This page is pretty good if you are a good
mathematician or an actuary
GENERAL EQUATIONS
FOR THE REPAYMENT OF DEBT
mathematician or an actuary
GENERAL EQUATIONS
FOR THE REPAYMENT OF DEBT
Until now, as far as I can tell, no one else has derived the general equations for mortgage and other debt finance based on a variable level of repayments. The main safe entry cost equation derived here gives insights into the stability or otherwise of pretty much every mortgage and debt model that has ever been tried.
Actuaries may remember the days when they studied the mathematics of Temporary Annuities.
PART 1
Introduction to Ingram's Risk Management Chart, the 'safe' area,
the standing loan line, and Payments Depreciation
Introduction to Ingram's Risk Management Chart, the 'safe' area,
the standing loan line, and Payments Depreciation
The rate at which the payout escalates depends upon the level at which the payments start.
A mortgage is an inverse annuity, so that much of the basic maths will be familiar.
Do you remember the way that for a temporary annuity at 5% interest you can pay a level amount every year? If you reduce the amount payable (the 'yield' percentage) by 1% p.a. you can increase those payments by 1% p.a. The fund will be exhausted of capital in the exact same time frame. A Mortgage repayment works the other way around. The fund borrowed is repaid in the exact same time frame. The similarity of the maths may explain why these are sometimes called annuity mortgages.
We will get that same result a little later for the repayments of a mortgage, or any fixed term debt.
MAIN MATHS
P% = P / L x 100% where
P = the current level of annual payments p.a.
L = the debt / loan / mortgage value
So 'P% p.a.' is the percentage of the debt 'L' that is being paid by money payments 'P' p.a.
r% = Nominal Interest.
NOTE: I often drop the 'p.a.' part as this is understood.
For example
If P = 7 p.a. and L = 100 (any currency) then
P% = 7% p.a.
If nominal interest rate r% = 7% and P% = 7% then only the interest is being paid. P% = r%.
e% p.a. = the rate at which debt servicing payments P p.a. increase every year. Remember P is NOT P%.
P = the annual amount of MONEY paid P% is the percentage of the debt being paid.
Example: if P = 100 and e% = 3% p.a. then at the start of the following year the value of P = 103.
AEG% p.a. is an index of average earnings growth - the definition for which is something that needs careful thought as discussed on the page entitled MATHS 3 - defining AEG/GDP
RISK MANAGEMENT CHARTS
Now we can draw this chart below.
FIG 1.1 Ingram's Risk Management Chart
Now we can draw this chart below.
FIG 1.1 Ingram's Risk Management Chart

The chart has two Axes, two straight dashed lines, one at 45 degrees slope representing a standing loan line and one vertical line representing the current rate of AEG% p.a., and an 'X' which describes the current state of any regular repayments loan.
The 'X' has a value of e% and a value of P% - as any debt repayments schedule has. Any place on the chart, and any regular repayment loan at all times has a value for P% and a value for e%. Both are p.a.
It is common practice when quoting interest rates to drop the 'p.a.' and I have done the same for whole equations when it is clearly understood that there is a 'p.a.' attached.
In the above example, FIG 1.1, the position of the 'X' is in the 'safe area'. This is because the 'X' lies to the left of the AEG% p.a. line and so the payments are rising more slowly than average incomes (AEG% p.a.) thus keeping arrears under control, And because the 'X' is above what I will explain is the standing loan line, so the debt is being repaid. This is the safe area of the chart.
If the 'X' was placed at the origin, the position of the 'X' would describe an overdraft: no payments, and no escalation e% p.a.
Anywhere on the Y-Axis is a 'Level Payments' Loan: no e% p.a. escalation of the payments is scheduled. Most lenders change the level of payments only at year's end. The payments level P% p.a. (and P p.a.) may jump up or down because those movements are not scheduled as a regular year end event.
If the 'X' is attached to the AEG% p.a. line (which moves when the nominal rate of interest changes) it is an earnings linked index-linked loan. That is to say that the capital value of the debt is rising at the same rate as AEG p.a. (Average Earnings Growth), Because AEG% is the rate of interest, the debt would be rising at a rate of AEG% p.a. if the 'X' was on the X-axix where no payments are made.
If the 'X' is on the AEG% p.a. line meaning that payments are being made, the total value repaid is equal to the number of National Average Earnings, NAE, borrowed. The NAE borrowed is the same in quantity as the NAE repaid. This is because as NAE incerases, so does the debt as interest at that same AEG% p.a. rate is added to the remaining debt every year.
The payments rise at the same AEG% p.a. rate do the amount of NAE repaid is the same every year.
Such mortgages are currently in use in Turkey where both the interest rate and the annual payments increase, are linked to AEG% p.a. / average incomes growth. In Turkey AEG is defined as the wages index of Civil Servants. And the mortgages are granted to civil servants.
So wherever it is placed, the position of the 'X' is the scheduled current condition of a particular debt repayment model.
The 'X' has a value of e% and a value of P% - as any debt repayments schedule has. Any place on the chart, and any regular repayment loan at all times has a value for P% and a value for e%. Both are p.a.
It is common practice when quoting interest rates to drop the 'p.a.' and I have done the same for whole equations when it is clearly understood that there is a 'p.a.' attached.
In the above example, FIG 1.1, the position of the 'X' is in the 'safe area'. This is because the 'X' lies to the left of the AEG% p.a. line and so the payments are rising more slowly than average incomes (AEG% p.a.) thus keeping arrears under control, And because the 'X' is above what I will explain is the standing loan line, so the debt is being repaid. This is the safe area of the chart.
If the 'X' was placed at the origin, the position of the 'X' would describe an overdraft: no payments, and no escalation e% p.a.
Anywhere on the Y-Axis is a 'Level Payments' Loan: no e% p.a. escalation of the payments is scheduled. Most lenders change the level of payments only at year's end. The payments level P% p.a. (and P p.a.) may jump up or down because those movements are not scheduled as a regular year end event.
If the 'X' is attached to the AEG% p.a. line (which moves when the nominal rate of interest changes) it is an earnings linked index-linked loan. That is to say that the capital value of the debt is rising at the same rate as AEG p.a. (Average Earnings Growth), Because AEG% is the rate of interest, the debt would be rising at a rate of AEG% p.a. if the 'X' was on the X-axix where no payments are made.
If the 'X' is on the AEG% p.a. line meaning that payments are being made, the total value repaid is equal to the number of National Average Earnings, NAE, borrowed. The NAE borrowed is the same in quantity as the NAE repaid. This is because as NAE incerases, so does the debt as interest at that same AEG% p.a. rate is added to the remaining debt every year.
The payments rise at the same AEG% p.a. rate do the amount of NAE repaid is the same every year.
Such mortgages are currently in use in Turkey where both the interest rate and the annual payments increase, are linked to AEG% p.a. / average incomes growth. In Turkey AEG is defined as the wages index of Civil Servants. And the mortgages are granted to civil servants.
So wherever it is placed, the position of the 'X' is the scheduled current condition of a particular debt repayment model.
THE STANDING LOAN LINE
The standing loan line is a line which, if the 'X' is placed anywhere on it, the loan will never be repaid. If the 'X' happens to be on the standing loan line then the value of the debt 'L' will be rising at the exact same e% p.a. pace as the payments 'P' are increasing.
This is how a standing loan is defined when payments are scheduled to rise at a constant annual rate. It is like a race in which the payments are rising as fast as the loan size is rising. Neither side wins. It is a dead heat.
To find out where that standing loan line may be we have to do some thinking. Refer to this page for the algebraic derivation. But there is a simpler way - just reduce P% by 1% for every 1% increase in e%.
What we just said in mathematical terms is this:
For a standing loan to exist, P / L = Constant,
and so P% = Constant.
The ratio P/L never alters.
Both variables change at the same percentage rate p.a.
For example, if P% = r% it is a traditional interest-only 'standing loan' in which case both P = constant, and L = constant. Both are equal to r%. No capital is repaid. Only interest is paid.
If P% is 1% less than the interest rate r% then what?
Then the loan size 'L' will be higher by 1% at the end of the year.
So the payment 'P' must increase by 1% to draw level and keep that ratio of 'P / L' unchanged for the start of the following year. At year end, after 'L' has increased by 1% 'P' has to catch up with 'L'. So e% = 1% p.a. at each year end. See FIG 2
FIG 2 - Standing Loan when e% = 1%
You can do the same for P% = 2% less than r%, so that 'L' finishes the year 2% higher. If you do that then 'P' has to rise by 2% to keep pace... See FIG 3:
FIG 3 Standing Loan at e% = 0%, 1%, and 2% p.a.
...and so on for all values of P% and e%.
The standing loan line is a line which, if the 'X' is placed anywhere on it, the loan will never be repaid. If the 'X' happens to be on the standing loan line then the value of the debt 'L' will be rising at the exact same e% p.a. pace as the payments 'P' are increasing.
This is how a standing loan is defined when payments are scheduled to rise at a constant annual rate. It is like a race in which the payments are rising as fast as the loan size is rising. Neither side wins. It is a dead heat.
To find out where that standing loan line may be we have to do some thinking. Refer to this page for the algebraic derivation. But there is a simpler way - just reduce P% by 1% for every 1% increase in e%.
What we just said in mathematical terms is this:
For a standing loan to exist, P / L = Constant,
and so P% = Constant.
The ratio P/L never alters.
Both variables change at the same percentage rate p.a.
For example, if P% = r% it is a traditional interest-only 'standing loan' in which case both P = constant, and L = constant. Both are equal to r%. No capital is repaid. Only interest is paid.
If P% is 1% less than the interest rate r% then what?
Then the loan size 'L' will be higher by 1% at the end of the year.
So the payment 'P' must increase by 1% to draw level and keep that ratio of 'P / L' unchanged for the start of the following year. At year end, after 'L' has increased by 1% 'P' has to catch up with 'L'. So e% = 1% p.a. at each year end. See FIG 2
FIG 2 - Standing Loan when e% = 1%
You can do the same for P% = 2% less than r%, so that 'L' finishes the year 2% higher. If you do that then 'P' has to rise by 2% to keep pace... See FIG 3:
FIG 3 Standing Loan at e% = 0%, 1%, and 2% p.a.
...and so on for all values of P% and e%.
Thus the standing loan line falls 1% for every 1% that the 'X' moves to the right.
Hence the Standing Loan Line forms an equilateral right angle triangle. The standing loan line is the hypotenuse and the axes form the two equal sides at right angles.
IMPORTANT NOTE: The standing loan line crosses both the Y-axis and the X-axis at the same value, r%.
Hence the Standing Loan Line forms an equilateral right angle triangle. The standing loan line is the hypotenuse and the axes form the two equal sides at right angles.
IMPORTANT NOTE: The standing loan line crosses both the Y-axis and the X-axis at the same value, r%.
A SAFE PLACE FOR THE 'X'
To make a loan affordable and safe the 'X' has to be above the standing loan line so that it gets repaid and it has to be to the left of the AEG% p.a. line so that the payments increase more slowly than incomes do - this way it gets easier to repay for an 'average' borrower every year.
Of course, such 'average borrowers' do not exist. A better way of thinking about this is to think of a fixed interest loan of the traditional kind when NAE, National Average Earnings, are rising every year.
The difficulty with that system, the one in use today in many countries, is that NAE can be rising at any rate, or not at all, or they can be falling.
With this new system we will be able to manage the relative rate at which earnings are rising, not by tampering with NAE, but by adjusting the level of payments - the distance between the 'X' and the NAE line. As long as we keep the 'X' above the Standing Loan Line, the debt will be repaid.
There is some difficulty in knowing what an average borrower is because incomes rise at different rates as people get older and they may rise at different rates in different states or regions of the same nation. This means that the distance to the left of the AEG% p.a. line needs to be enough to cope with those and any other systematic unknowns.
AN ORDER OF MAGNITUDE SAFER
If we can manage to do this, then this new way of managing the repayments is far and away safer for borrowers and lenders (who hate chasing arrears and having non-performing loans), than the traditional model for repayments. In the traditional model, payments on a newish loan can leap up by 20% all in one go, regardless of the fact that incomes may be barely rising at all.
ILS RESCUE MODEL
All of these new models are calles ILS Models based upon this 'Ingram's Lending and Savings 'mathematics. There are variations of the new model which can cope with that kind of situation. It is called the 'ILS Rescue' Model.
The borrower is using the traditional repayments model but instead of the payments leaping up by 20% as the rate of interest rises by around 2% on the new 25 year loan, what happens is that the payments rise by 2% p.a. and as we know from annuity mathematics, the loan will be repaid on time. It may take almost ten years for the repayments to rise by 20%. By then the borrower's income can be much higher and well able to cope. By then interest rates may have fallen. If they ris again it is likely to be because the rate of inflation and AEG% p.a. has risen. The chance of a rescue is close to 100% if the borrower continues to have income. That home will not be repossessed because the payments leapt up out of reach.
GOING BACK TO THE STATISTICS
When it comes to selecting the best index to use for raising the level of repayments, the median rate of growth of earnings may be more representative of how fast a typical borrower's earnings may be rising than the average rate. The average rate seems to favour the top 1% in recent years in the USA for example. There are plenty of variations. However, the maths says that we must chose some index - some measure for the rate of increase in average borrowers' earnings.
If the payments do not get easier every year, compared to that chosen index, that is if the 'X' is on the AEG% p.a. line, you have the Turkish Wages-Linked Mortgage Model as already mentioned, where the payments increase at the same rate of increase as the wages index that they use. This creates 'Payments Fatigue' and limits the amount that can be lent safely. And it does not take account of people whose incomes are rising less quickly than the index. Because not all incomes rise as fast as the index, this, and payments fatigue, is likely to increase the level of arrears and defaults which otherwise may be close to zero.
This mathematics is used to create the Ingram ending and Savings (ILS) Models for finance - any form of fiance.
PAYMENTS DEPRECIATION D% p.a.
The Ingram Savings and Lending (ILS) Mortgage Model inserts a figure, D% into the equation used to calculate next year's repayments level.
D% is the horizontal distance of the 'X' from the AEG% p.a. line. D% p.a. is called the rate of Payments Depreciation. The larger the value of D% (the greater the distance the 'X' is to the left of the AEG% line), the faster the payments get easier as a portion of the 'average' borrowers' income, whatever that means. To have an average borrower, one has to create an index of average borrowers' incomes. For a discussion on this topic please refer to this page entitled MATHS 3 - Defining AEG / GDP.
Having a positive D% avoids payments fatigue and minimises the level of arrears. Clearly, for a non-average borrower each borrower will have his/her own D% value.
CALCULATING D% The important point is to the payments becoming easier every year for say, 95% of borrowers. Or failing thatm to have this happen in most years.
That means doing some researches on a lender's mortgage book - the way in which those actual borrowers' incomes are likely to behave going forward - how much the deviations from your average income the individuals will stray. You can try doing a survey and using Standard Deviation and Mean calculations.
This may help to determine a practical minimum value for D%. For example, if 95% of borrowers' earnings are rising at a rate which is within 2% of AEG% p.a. then a value of D% which is above 2% will ease the burden of payments for that 95% of borrowers.
It is also important that this happens for borrowers during the early years. Later on the value of the debt is less and payments can be rescheduled over a longer period very easily. So a high 'D%' value in the first year can be safer than a constant 'D%' value every year.
Another safety margin can be created by allowing the total repayments period to vary. A short addition to the repayment period can make a large difference to the payments increase needed.
This is also one reason for lending over 25 years rather than over 30 years or more. An extension to 30 years can help a great deal if a borrower needs help.
Adding in the value of D% (placing the 'X' to the left of the AEG% p.a. line has the effect of increasing the initial cost 'P p.a.' of the mortgage. This first yeat payments level is called the Entry Cost of a Mortgage. Hopefully it will also be the Safe Entry Cost by the time we have done all the researches needed.
For every 1% value given to D% p.a. the entry cost P% p.a. rises by 1% p.a.
P% = C% + D% + I% - Ingram's Safe Entry Cost Equation
See PART 2 for the derivation.
SUMMARY
So far we have established the components of the Risk Management Chart, the fact that we can draw a standing loan line which slopes downwards at 45 degrees, and crosses both Axes at r%, the level of the nominal rate of interest.
This means that the vertical and horizontal sides of the triangle, formed by the standing loan line with the two axes, have equal sides.
We have also placed an AEG% (Average Earnings / Incomes Growth) line on the chart. We know that this line moves to the left and to the right as the value of AEG% p.a. (the rate of average earnings growth) changes.
The reason for calling it Average Earnings Growth is that when these studies first began there was no incomes index in the UK, only an earnings index. It may prove to be more practical to replace AEG with AIG - Average Incomes Growth because many borrowers will not have additional earnings from rentals and dividends, royalties, etc.
We have not yet found out much about that entry cost equation but it is clear that if the equation for P% is correct, a 1% rise in D% adds 1% to the entry cost. It is a very simple and neat relationship which we will be using in the management of arrears risk.

Here in FIG 2.1 are three new letters:
C% = the distance of the 'X' above the standing loan line. This is a form of capital payment which ensures that the loan will be repaid. The value of C% largely determines when the debt will be fully repaid.
As time passes the loan gets smaller, the interest component of the repayment gets smaller, and C% gets larger. As more capital value is being repaid less of the payments P are used to cover the interest added.
D% = the distance of the 'X' to the left of the AEG% p.a. line as already explained. As long as D% is a positive figure, this ensures that the payments will increase more slowly than average incomes. This is called the rate of Payments Depreciation, D% p.a.
NOTE the precise definition of D%:
D% = AEG% - e% - (ii) - all are p.a.
DEFINITION
I% = r% - AEG% - (iii) as shown on the chart
or if preferred:
r% = AEG% + I% - it means that the nominal interest rate r% is the sum of these two components.
If you have been reading the economics paper, the core part of the interest rate adjustment is AEG% p.a.
The real economic part, which adds value (NAE) to the debt, is I% p.a.
Remember, if interest is added at AEG% p.a., then the total sum repaid is equal to the number of NAE borrowed in the first place.
All of these variables are p.a.
FIG 2.1 again

This third distance I%, could just as easily have been shown on the Y-axis but there is a reason for placing it on the X-axis.
I% is called the 'true' rate of interest and is defined as the marginal rate of interest above AEG% p.a:
For example, if I% = 0% it means that the interest added to the loan is equal to the rate at which average earnings / incomes are rising, AEG% p.a.
Because this is NOT the real rate of interest which is the marginal rate above a prices index, it needs a new name. Because there is no such name in the dictionary, I have called this the True rate of interest.
Given the three new variables, C%, D% and I%, seen in the last chart, we can link them together like this (see the explanation below - it is easier than the summary on the chart).
FIG 2.2 - Derivation of P% = C% + D% + I%
 Note that there are two small equal sided right angle triangles:
Note that there are two small equal sided right angle triangles:
One with two sides of I% shown by the double headed arrows
and
One with two sides of D% again shown by double headed arrows.
Hence by adding up the vertical distances we can see that:
P% = C% + D% + I%
WHAT THIS EQUATIONS TELLS US
This means that ALL debt repayment schedules have these three parts, C%, D%, and I%, whether intentionally or not. It may be a Level Payments Loan, (an annuity loan), or a standing loan, or an overdraft or an ILS loan. Whatever the contract may say there is a place on the chart with a value of P% and a value of e%. Therefore P% can be divided up into these three elements.
There is no debt repayments schedule which has no value of e% or no value of P%. Since all debt repayment schedules have a value P% and a value e% they also have a value for C%, D%, and I%.
This means that any current loan repayments schedule can be converted into an ILS repayments schedule, which as explained above, may result is a rescue for both lender and borrower.
Even if e% = 0% as with Level Payments, the location of the 'X' that describes the repayments is on this chart and so P% contains a value for D% and a value for C% and a value for I%.
One interesting thing that I tested was whether the level payments equation is a special case of the general equation.
So let us put e% = 0 % in this equation. We already have:
D% = AEG% - e% - (ii)
So this means that when e% p.a. = 0% p.a. we have:
D% p.a. = AEG% p.a. - (equation x say)
Now we have: P% = C% + AEG% + I%
We also know that
I% = r% - AEG% - (iii)
which using (x) for D%, and (iii) for I% gives:
P% = C% + AEG% + r% - AEG%
So P% = C% + r%
Which is indeed the equation for an annuity mortgage with level payments. You pay capital plus interest.
I wanted to know how P% would vary as AEG% p.a. changed. There is no change in P% when AEG% varies. The entry cost is the same no matter what the rate of inflation of earnings (and everything else). So then the amount lendable is also the same for any goven income. Here's the proof:
By removing the Y-Axis we get the same equation for P% but there is no change in P% as the value of AEG% varies. We can re-draw the chart like this:
FIG 3.1 - Ingram's Risk Management Chart (Relative)
Everything is relative to AEG% p.a.
In the economics papers, AEG is like the rate at which the KFPP platform is rising. or the ship is rising as the water level changes. With all of the passengers, P%, C%, D% and I%, on board, none of them notice the tide or the pace at which the KFPP platform is rising.
People are wholly unaffected.
But of course, in the real world, not all incomes and prices rise at the same time. It is better to have a low rate of devaluation of money / price rises.
The difference between a theoretical economy in which money never falls in value and AEG% p.a. = 0% p.a. and a real economy which is financially stable, is that theroetically every cost, price, earnings, and value, rises at the same AEG% p.a. rate. In practice some of these prices (all are a form of price paid for something including the cost of hiring a person or an enterprises), do not take place on the same day. So real economies cannot be entirely financially stable. Some people get an advantage over others during the adjustment period. Otherwise, as AEG% p.a. reduces these differences also reduce and in theory at AEG% p.a. = 0% p.a. they all vanish.
What keeping pace with AEG% p.a. means is that the value of something keeps pace with everything else and the costs also keep pace. The effect of the falling value of money is neutralised.
It is the same for pension funds - they also want to be on board this ship / platform. They want to keep pace with AEG% p.a. So if they are financing the mortgages they can offer a loan at a fixed rate of I% interest with the capital then rising at AEG% p.a.
r% = AEG% p.a. + I%.
They just need to see that I% is positive and they will sit there on board the ship collecting I% interest whilst adding AEG% interest to the capital debt. The caital lent will keep pace with NAE and the interest can be used to pay for administrtion and risk.
If AEG% reaches zero, if money has a constant value, (not constant purchasing power which is different), then I% = r% - the nominal rate of interest. Remember:
r% = AEG% + I% by definition.
What has happened with this safe entry cost equation is that incomes inflation has been taken out of consideration. Everything works the same as if AEG% p.a. was zero. C%, D%, and I% are not altered. P% is the same. The safe entry cost for a loan is the same. The amount which a person can afford to borrow is the same because the entry cost is the same.
What if AEG% p.a. goes negative?
Nothing changes. The relative chart is the same. The 'ship' goes downwards. Everything is on board. The repayment term, being governed by C% is the same. As always, D% will be unchanged and positive. The payments will be falling at D% faster than national average earnings are falling. An economic depression with not harm the borrowers on this side of their expediture. Lenders ill have fewer problems with arrears.
Lets us look at some examples of ILS Loans with various rates of AEG% p.a. Here, incomes are not rising but the payments are falling. The nominal rate of interest is low at 3% but that is not low for I% based on past data for three nations studied. It is average in al three nations over the period before we had super-low rates of interest in the erly 2000s and asset prices inflated and, and, and everything went wrong.
FIG 3.2 - ILS Mortgage with AEG% = 0% I = 3%
Note that the payments fall every year and that the '% of income' used every year falls to 11.26% in the final year.
CONVENTION USED
NOTE: when we say '% of income' we are taking a percentage of a standard income which is defined as one which changes at the rate of AEG% p.a.
The borrower's income could start out as 1 NAE - one National Average Earnings / Income (1 NAI), and so the amount borrowed would be 3.55 NAE in this example. See bottom line, first column where it says 3.55 times income as the size of the loan.
This means that all of the '% of income' data is a percentage of 1 NAE. In this example the total cost would have been 4.80 NAE as shown in the 'Total in Yrs of Income' cell.
This is how that payments schedule looks:
FIG 3.2a - AEG% = 0% I% = 3% BARS for '% of Income' as cost.
Again, the bars represent the falling number of NAE being repaid. If the borrower's income is more than 1 NAE then the loan is that much larger and the bars are that much higher but the shape of the bar chart is the same.
Now if we examine what happens if AEG% is high, at 9% p.a. we get this:
FIG 3.3 AEG% = 9% I% = 3% as before
The same pattern appears in the final column. Compare the numbers with the previous tabulation above. And the amount lent is about the same as before with the entry cost also about the same as before.
NOTE: If the table did not use annual intervals but daily intervals to apply interest and payments it is thought that the amount borrowed would not be different as AEG% p.a. changes. That is a challenge for some clever reader to prove.
The net cost in terms of total number of years of the borrower's income paid as interest is 32.7% interest on the loan, being the total cost of 4.55 years' income, less the amount of 3.43 years' income originally borrowed. This is similar to the previous example.
There are slight differences in the figures, which I must ask an actuary to explain! See the note above.
But broadly speaking nothing much has changed. Unless, that is, you look at the money data which is totally different. The net cost is now 317% of what was borrowed whereas previously it was 35.2%. Counting the money cost is highly misleading.
If we try the same tabulation with D% = AEG% = 4% and I% = 3% we get the Level Payments Model with r% = AEG% + I% = 7% as before. This is because in all of my illustrations I have set D% at 4% p.a. If AEG% = D% we have the level payments model.
FIG 3.4 - This is another ILS Model but it could also be the Level Payments Model at AEG% = D% = 4% and I% = 3% again. That is because in the LP model AEG% = D% and e% = AEG% - D% = 0% in that case.
Check out all the figures in the bottowm row. Only the money figures look much different.
The BAR charts of FIG 3.2a would all look very similar for all of the above examples. If you looked only at the bar charts, as long as D% = 4% and I% = 3% in every chart, you would not know the value of AEG% p.a. The bar charts all look the same. They show the % of income figures.
FIG 3.5 - Incomes falling
The standing loan can be extended to the left of the Y-axis too.
The value of P% is not any higher just because the 'X' is to the left of the Y-axis because this condition lowers the value of r% - unless there is something distorting interest rates! We will be looking at the behaviour of interest rates.
If readers look again at Table 3.2 this illustrates this chart with the 'X' exactly where it is here.
The key to note is that I% p.a. is the rate at which NAE is added to the mortgage debt, L, expressed in units of NAE.
I% provides a positive true rate of return / interest to the lender / investor.
Any higher than that indicated by Siegel's Constant and the level of demand will generally bring the true rate of interest back down. Besides that, the higher the value of I% the fewer borrowers there will be wanting to borrow.
Here are some interesting case studies of how the money looks in various scenarios:
to be continued shortly
=============================
What happens if D% = 0%?
If we are to compare the arrears risk of various mortgage repayment models we have to look at the likely behaviour of D% as we endeavour to keep the repayments on schedule without interfering with either C% or P%.
Given that D% needs to be positive, we can decide which debt repayments models are safe and which are not. Those that have no control over D% are not safe - at least not for people. A government can mange with D% = 0% without getting payments fatigue because tax revenues go on and on and should never depart too far from AEG% p.a. even in a recession.
Over short periods there is likely to be a strong relationship between AEG% p.a. and the rate of change of Nominal GDP, but if a large part of the working population jumps ship / emigrates, or if unemployment rises significantly, there will be some divergence.
Since the value of D% is the distance of the 'X' from the AEG% p.a. line, it follows that if e% = 0%, as it is with a fixed interest mortgage or a fixed interest government bond, then since the AEG% p.a. line is always on the move, the value of D% p.a. is always on the move.
In fact, AEG% p.a. can go negative as it has done in some European countries recently.
The effect on this of I% can be very nasty. Remember:
I% = r% - AEG% - (iii)
For example, if r% = 3% nominal interest
AEG% = -5% p.a.
You get I% = 8% p.a.
That is 8% of the income borrowed added to the debt by the true rate of interest. A debt of 4 times income then rises at 4 x 8% = 32% of income p.a.

The mortgage schedule begins to look like this:
This also affects an investment in a government bond hugely during a slow down or a recession. Below is a graph showing how that has affected the return on US treasuries on a year by year basis since 1980 when inflation was high and since when it has fallen to almost zero. The effect is the same:
Try r% = 20% and then AEG% falls from 25% to 11%. You get I% = 20% - 25% at first = -5%
But then this becomes
I% = 20% - 11% as inflation comes down = 9%.
This is like what happened to USA Government Bonds and the result was this graph:
As can be seen the return on USA AAA rated bonds reached 25% one year and averaged something like the trend-line shown. This average reflects the cost to USA tax payers of using fixed interest bonds over that period.
This additional GDP added to the total government debt is probably enough compounded up to explain most of the rise in USA government debt since that time! For example, 5% p.a. compounded over 25 years comes to a 3.6 fold increase in the original number of GDP owed in 1980 if no repayments were made. Certainly 9% true interest would not have been paid. Some part of it maybe would. Even paying 5% is steep.
THE DANGER OF A BOND CRISIS
Now that interest rates are virtually zero there is a significant danger that the value of these bonds may collapse when Quantitative easing is reduced and interest rates rise. This can produce another world crisis of enormous proportions and is the worry of one Andy Haldane at the Bank of England as expressed in The Guardian newspaper recently (before this weekend of 15th June 2013). His remarks may be enough to cause another panic - we will see.
The interest rate sensitivity of mortgage finance is also very great and it is this which accounts for the rise and fall of property prices and which can also undermine the whole economy.
In both cases we need to reform the debt structures.
IN SUMMARY
The cost-to-income of the fixed interest mortgages or even the low interest rate mortgages rises every year if average incomes are falling. The same applies to government fixed interest rate debt / bonds. The cost rises every year. This is not safe, and it leaves investors not knowing what kind of I% they will get on their investments. If a recovery comes then I% can even go negative. So this arrangement is not safe for borrowers or for investors / lenders.
Given the amount of wealth invested in both housing and government bond sectors this is very distressing to the performance of the whole economy.
What we are looking for is a repayments model which looks something like the sketch already presented twice now:
Repayments follow a more 'normal' rental type model, rising with incomes but not quite as fast.
Looking at the equation:
P% = C% + D% + I%
we see that adding in D% to get this slope adds to the value of P% - the initial cost of the repayments.
Putting D% p.a. = 4% adds 4% to P%.

Such a repayments model might look like this if I% had been fixed at 3%. (I% can be fixed by offering fixed true rate wealth bonds to investors).
The downwards slope means that D% p.a. is positive. In this illustration the payments start at 30% of income and reduce at 4% p.a. to reach around 11% at the end of 25 years. The slope is the value of D% and so it is based on the AEG% p.a. index of incomes, not individual incomes. But if the slope is steep enough all borrowers within reason should be able to cope with the repayments.
In practice the straight sloping line should be curved, but it helps to make the point when I do not show the curves of compounding.
Let's do a short revision course.Originally I wrote the following script about the fixed interest mortgage model - it goes over what I just wrote above, but in a different way:
Given that, by definition:
D% = AEG% - e% - (ii)
we can see that fixing e% = 0% can lead to problems when AEG% is close to zero because if e% = 0% for level fixed payments and AEG% = 0%, then D% = 0%.
Example for austerity:
AEG% = -2% and e% = 0% gives:
D% = - 2% - 0% = -2%
So as already mentioned above, the payments are costing a 2% higher proportion of average income every year. Like this:
It helps to make the point when I do not show the curves of compounding.
Here D% p.a. is negative so the slope is up instead of down and payments are rising relative to average income every year.
What is worse is that the value of I% also rises. I% governs the cost-to-income that the borrower has to repay. I% adds wealth to the wealth debt already owed. Suppose that the lender offered a fixed rate of nominal interest with r% = 3% but then AEG% fell to -2%. We know that:
I% = r% - AEG% - (ii)
So I% = 3% - (-2%) = 5%.
This is more costly to the borrower than raising equity capital. For lenders 5% above AEG% p.a. pays better than investing in equities and property. I am assuming the equities investment data on that for the USA / UK applies here.
For other nations lenders need to do more researches to reach their figures. But normally one would expect a high rate of return that out-performs long term investments in equities and property to lead to major problems for prospective new borrowers and a flood of money on the books of lenders which they would not be able to lend.
As already noted, normally the value of I% (net of lending costs and taxation) should not exceed the rate of return on such other investments but it should also be above zero to limit the demand for borrowing.
PREVENTING THE NEXT CRISIS
Imagine that a UK lender was to offer a 10 year fixed true interest rate of 5% p.a. The number of older people wanting a safe investment that performed that well would be very high. It would provide a very safe annuity. I have listed a whole range of uses for this kind of bond on this page called NEW FINANCIAL PRODUCTS RESULTING.
As soon as these kinds of wealth bonds become available there will be a major clamour for such products because nothing sells better than risk free (to wealth) investments. But to make that happen in time to prevent Andy Haldane's feared crisis there needs to be a commission of enquiry set up and an IMPLEMENTATION programme developed as outlined on that same blog.
There we are discussing the replacement of fixed interest bonds with wealth bonds in a very different environment of low true interest rates - but safe wealth will attract a massive demand at an rate of true interest in the environment that currently prevails. Doing so will safeguard the banks' balance sheets. Offering the replacement wealth bonds at a discounted price would cut the government's debt.
Investors face the alternative of imploding bond values as interest rates rise, so a discounted rate may well be popular.
Going back now to looking at the upper boundary for I% in more normal economies:
The number of borrowers wanting to borrow at a 5% level of I% would be much fewer because the slope for D% p.a. would reduce to 2% p.a. compared to the illustration above:
P% = C% (about the same) + D% (2% less = 2%) + I% (2% more).
By keeping C% the same the total repayment period would remain close to 25 years. To do that D% has to drop to compensate for the higher level of I%.
Then we get this:

The slope is 2% less and the total cost is a lot more.
I will come back to this a bit later with more detail.
CONCLUSIONS
1. A fixed interest mortgage does not look viable when AEG% p.a. is falling. For another example if AEG% = 10% and r% = 13% fixed, what happens when AEG% p.a. falls to 5%?
I% = 3% at first but then rises to 8%.
This is similar to what happened to the USA government bonds in the 1980s. See above. It meant that AAA rated bonds were yielding far more than share investments ever did over the longer term.
2. If we look at the main equation:
P% = C% + D% + I%
We can see that a rising level of I% requires a lower value of D% if P% and C% and the total repayment term are to remain the same.
In fact if I% increases by 1% the D% must decrease by 1% or the mortgage will go off schedule as C% adjusts instead. Or P% will rise - taking us back to the same old problems that we are having with variable interest rate mortgages now.
For the moment let us not look at variable rates. Above we are looking at fixed true rates. So if the fixed true rate on offer to lenders out there in the market for say 10 year bonds or longer, rises by 1% then D% will fall by 1%.
I named the main equation P% = C% + D% + I%
Ingram's Safe Entry Cost Equation because it can be used for setting the entry cost (the initial value of P%) and because I was unable to patent it I attached my own name to it.
Interestingly the value of P% does not depend upon the value of either r% or AEG%. It depends on I% which is the difference - the marginal rate at which NAE gets added to the debt.
I% = r% - AEG%
So the rate of inflation, or AEG% p.a., in a nation should not affect the amount that can be lent safely - by much.
The most important difference would be the variability of incomes growth between different members of the working population. If this gets too big then it needs a larger D% to accommodate it.
In fact this is a general equation which can be applied at any time to any form of regular payment debt. It takes the basic elements of Payments Depreciation, D% p.a. Capital repayments C% p.a., and wealth addition (I% p.a.) and adds them together to get the cost of the payments P% p.a.
P% = C% + D% + I% - all are p.a. - (i)
First, some more revision...REMEMBER:
I% is not the nominal rate of interest 'r%'; it is the marginal rate above AEG% p.a. I called this the True rate of interest.
I% = r% - AEG% - (ii)
ABOUT TRUE INTEREST I%
When the interest rate = AEG%, say 4% p.a. and incomes are rising at the same 4% p.a. the amount owed at the end of the year is 104 per 100 debt.
But if incomes also rose by 4% the debt / income ratio is no higher:
If income was 100 at the start of the year it will also be 104 by the end of the year.
So a year's income was borrowed and even without making any repayments at all, the loan will still be one year's income at the end of the year.
Only the excess interest above AEG% p.a. increases that ratio. Only that excess (marginal / true) interest adds to the cost of borrowing for a person on average income increases.
If r% = 10% then the loan will be 110 at the end of the year and if incomes are rising by only 4% p.a. then income will be 6% less at 104.
I% = 6%
At this rate the income owed increases by 6% p.a. compared to the income borrowed. But we are talking here of average incomes...
BORROWERS V INVESTORS
New script
What the borrower sees and what the investor / lender sees are not the same.
We can think of borrowers as not all getting average income increases. For those with incomes growing less quickly the cost-to-income will be higher. For those with incomes growing more quickly the cost-to-income will be lower.
For the investor looking to lend money and to preserve the years of income that has been saved and lent, they want to keep pace with, or do better than, the average / the index, much as they may expect to do over the long term with equities or property. All have a loose link to AEG% p.a. the aggregate demand baseline of economies.
However, market forces, or counter-inflation policy, will determine the interest rate unless it has been distorted by something.
DEFINING WEALTH
So let us define wealth as the number of years' income that has been lent.
This definition of wealth is useful because when I% is positive it moves wealth from the 'average borrower' to the investor. In this sense, wealth can be defined in units of National Average Earnings, NAE.
NAE is the part of the national income that a person has earned as income or profits, or has been given, or acquired in some way.
If that part of National Income is not preserved when it is invested, some other person or entity will spend the part that has been lost.
For example, look at this spreadsheet which is produced by the EXCEL sheet mentioned earlier as being for sale:
FIG XX - Negative true interest moves wealth from lender to borrower
The wealth lent was 4.23 years' income. The wealth repaid is found by adding up the '% of income' numbers which comes to 320% or 3.20 years' income as shown. This is 1.03 years' income less wealth / income than was borrowed, as shown. The net cost of borrowing is -24.3%.
This income (wealth) has not been lost. The borrower first spent the income (NAE) that he/she borrowed / was lent, and then repaid less NAE so he/she was able to spend the income / wealth (NAE) saved on something else. The table does not show the NAE but one could try this: assume that the borrower was on average income and then the table does show NAE. 4.23 NAE was borrowed and 3.20 NAE was repaid.
Wealth did not vanish - it moved. 1.03 NAE moved from the lender to the borrower.
The same applies if I% is positive - wealth moves but this time in the other direction.
TAX DISTORTION
If we look at the MONEY repaid in the above illustration it looks like a 77.4% profit. That gets taxed - haha! Some joke. Some distortion.
Distortions all cost the economy and the social fabric something, so we will need to look into this and see how we can sort it out without messing anything up. It can be done.
In America they give tax relief on the interest paid! Giving tax relief on AEG% of the interest is a variable rate gift and another distortion. It is not needed. The net result of both tax regimes combined (taxation of all interest and tax relief on all interest), is to tax saved wealth and give it to borrowers. It reduces the ability of lenders to keep interest rates down. The main effect is to increase administration costs.
In reality, in the above scenario (see the table again), the borrower spends the 4.23 years' income right away and only has to repay 3.2 years' income leaving him/her free to spend the remainder at will on whatever is wished.
A year's spending power has left the lender and moved to the borrower.
Imagine if the borrower's property has risen at the same rate as AEG% p.a. That is quite possible, even probable. He/she will do very well.
TRUE COST DEFINED
If I% is positive, we now can see that the cost-to-wealth of the repayments, as opposed to the cost-to-income of a particular borrower, is the true cost (actual cost to wealth). The true cost is not the cost to the income of a particular borrower. It is the wealth that has been borrowed plus the overall cost of the marginal interest rate I% which has increased the wealth owed and added to the wealth of the lender.
TWO MEASUREMENTS
In all my spreadsheets readers will find two cost figures:
There is the money cost and
There is the wealth cost, or the 'true cost' as I call it. This is the number of year's income that it takes to repay if the borrower's income rises as fast as average. True cost can also be expressed in NAE. For governments it can be expressed as a fraction or a percent of GDP.
The two figures, money cost and true cost usually look very different.
When inflation is high and interest rates are high the cost to money can be very high indeed, yet at the same time the cost to income can be very low or even negative.
This means that the figures offered to the public can be very misleading.
Even if the figures are adjusted for prices inflation they can be very misleading:
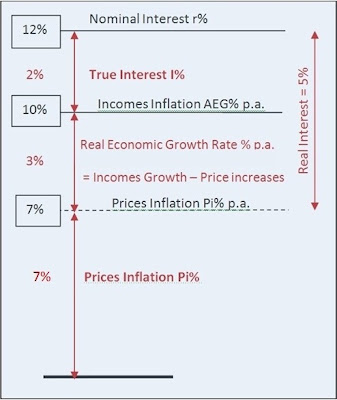
Here the nominal interest rate is 12% and prices inflation is 7% so the real interest rate is 5%:
12% - 7% = 5% real interest.
But the true interest rate is only 2%:
12% - 10% (AEG%) = 2%
If the nominal interest rate had been 8% then the real interest rate would have been +1%:
8% - 7% inflation = +1% real interest
but the true interest rate (I%) would have been -2%
8% - 10%(AEG%) = -2%
8% interest means that a loan of 100 becomes 108 at year's end
But incomes would be 110 by year's end.
So now we see that the average borrower will not need to repay the whole year's income that was borrowed. 2% less wealth will need to be repaid than was borrowed just in that one year. Yet the real rate of interest was +1%. Real interest does not protect wealth.
So an index-linked investment which is linked to prices does not protect wealth.
You do NOT find that in your text books!
MISSING TABLE
I compiled a table to show how much 'wealth profit' an investor can get from buying a fixed true rate bond at various rates of interest and I included the cost to a borrower over a 25 year term from borrowing at the same rates of interest. I will add this table when I locate it. I gave an example of 5% true interest increasing wealth by 3.6 fold though. So it can be seen that quite small amounts of true interest are very attractive to older people seeking security.
THAT EUREKA THING
NOW we see why it was so important to introduce I% into the main equation. I% is the rate of wealth transfer. A high I% is a serious factor in any debt repayments schedule. Wealth as measured / added by I% is a real and tangible thing that has never been declared in our text books.
And it brings to the fore the importance of AEG% as a baseline for everything in the economy - all forms of investment are propelled by AEG% p.a. - by aggregate demand and how fast it changes.
If we adjust all prices and repayment costs for AEG% p.a. everything will be seen as if there was no AEG% p.a. Everything is relative to AEG% p.a. Only the excess I% adds a cost or a benefit. Only I% moves wealth.
SUMMARY
True interest is a key component of the economy. It is responsible for wealth transfer on a massive scale, even when it is not very high.
The text books are not telling it as it is when they write of real interest rates. Real interest rates do not preserve wealth.
A true rate of interest of zero incorporates the real rate of economic growth (approximately) and is a great selling point to raise funds for lenders - and for governments. Yet it costs the borrowing house buyer or government no actual wealth.
Eureka! - What have we been thinking all this time?
The data that I have for the UK shows that the true interest averaged +3% on home loans from 1970 to 2002. I got a similar figure for South Africa and I used this 3% figure to forecast by how much the Fed might need to raise interest rates in 2006 / 8. My forecast was almost exactly in line with what was actually targeted. It was just that to target such a 4.5% raise in interest rates implied a 58% increase in the cost of variable rate prime mortgage payments!
I wrote this page on Finding the Mid-Cycle Rate of Interest as a result of that calculation / observation.
Clearly, you cannot lend a whole lot more just because, temporarily, interest rates have fallen, no matter how far they have fallen.
So I have used 3% true interest as a baseline for my studies and simulations - the assumed average rate. Readers can experiment with other average rates and I have done that too. My spreadsheets are available for sale. So given that baseline:
Given that P% = C% + D% + I%
We can put in some figures:
P% = 1.5% + 4% + 3% = 8.5% p.a.
This is approximately the data that represents a 25 year mortgage repaid with 4% p.a. Payments Depreciation and at 3% true interest.
It creates a mortgage of 3.5 times income.
This is the original 3.5 times income mortgage that I illustrated above where the payments fell at 4% p.a. and which cost 30% of income falling to around 11% of income (shaded area) when I% = 3%.
If the true interest rate I% is 5% this means that D% now has to reduce D% from 4% p.a. to 2% p.a. because I% is 2% higher:
P% = 1.5% + 2% + 5% = 8.5% as before - so we still have a 3.5 times income mortgage because the entry cost is still the same.
 We cannot reduce C% because that will cause the loan to take longer to repay.
We cannot reduce C% because that will cause the loan to take longer to repay.
We do not want to increase P%, because that will hit collateral security / house prices, (but we can lean that way), so what is left is D%. This value must fall by 2% if I% rises by 2% as shown in this sketch.
Tests show that if the current true rate of interest is +11% or -7% (two extreme figures taken from South African data), the entry cost can still be set close to this mid-cycle figure because such extremes reverse and go the opposite way. The true rate still averages about the same figure.
I will add some back-testing data on a new page when I have time. It is already there for customers on the spreadsheet.
To make a loan affordable and safe the 'X' has to be above the standing loan line so that it gets repaid and it has to be to the left of the AEG% p.a. line so that the payments increase more slowly than incomes do - this way it gets easier to repay for an 'average' borrower every year.
Of course, such 'average borrowers' do not exist. A better way of thinking about this is to think of a fixed interest loan of the traditional kind when NAE, National Average Earnings, are rising every year.
The difficulty with that system, the one in use today in many countries, is that NAE can be rising at any rate, or not at all, or they can be falling.
With this new system we will be able to manage the relative rate at which earnings are rising, not by tampering with NAE, but by adjusting the level of payments - the distance between the 'X' and the NAE line. As long as we keep the 'X' above the Standing Loan Line, the debt will be repaid.
There is some difficulty in knowing what an average borrower is because incomes rise at different rates as people get older and they may rise at different rates in different states or regions of the same nation. This means that the distance to the left of the AEG% p.a. line needs to be enough to cope with those and any other systematic unknowns.
AN ORDER OF MAGNITUDE SAFER
If we can manage to do this, then this new way of managing the repayments is far and away safer for borrowers and lenders (who hate chasing arrears and having non-performing loans), than the traditional model for repayments. In the traditional model, payments on a newish loan can leap up by 20% all in one go, regardless of the fact that incomes may be barely rising at all.
ILS RESCUE MODEL
All of these new models are calles ILS Models based upon this 'Ingram's Lending and Savings 'mathematics. There are variations of the new model which can cope with that kind of situation. It is called the 'ILS Rescue' Model.
The borrower is using the traditional repayments model but instead of the payments leaping up by 20% as the rate of interest rises by around 2% on the new 25 year loan, what happens is that the payments rise by 2% p.a. and as we know from annuity mathematics, the loan will be repaid on time. It may take almost ten years for the repayments to rise by 20%. By then the borrower's income can be much higher and well able to cope. By then interest rates may have fallen. If they ris again it is likely to be because the rate of inflation and AEG% p.a. has risen. The chance of a rescue is close to 100% if the borrower continues to have income. That home will not be repossessed because the payments leapt up out of reach.
GOING BACK TO THE STATISTICS
When it comes to selecting the best index to use for raising the level of repayments, the median rate of growth of earnings may be more representative of how fast a typical borrower's earnings may be rising than the average rate. The average rate seems to favour the top 1% in recent years in the USA for example. There are plenty of variations. However, the maths says that we must chose some index - some measure for the rate of increase in average borrowers' earnings.
If the payments do not get easier every year, compared to that chosen index, that is if the 'X' is on the AEG% p.a. line, you have the Turkish Wages-Linked Mortgage Model as already mentioned, where the payments increase at the same rate of increase as the wages index that they use. This creates 'Payments Fatigue' and limits the amount that can be lent safely. And it does not take account of people whose incomes are rising less quickly than the index. Because not all incomes rise as fast as the index, this, and payments fatigue, is likely to increase the level of arrears and defaults which otherwise may be close to zero.
This mathematics is used to create the Ingram ending and Savings (ILS) Models for finance - any form of fiance.
PAYMENTS DEPRECIATION D% p.a.
The Ingram Savings and Lending (ILS) Mortgage Model inserts a figure, D% into the equation used to calculate next year's repayments level.
D% is the horizontal distance of the 'X' from the AEG% p.a. line. D% p.a. is called the rate of Payments Depreciation. The larger the value of D% (the greater the distance the 'X' is to the left of the AEG% line), the faster the payments get easier as a portion of the 'average' borrowers' income, whatever that means. To have an average borrower, one has to create an index of average borrowers' incomes. For a discussion on this topic please refer to this page entitled MATHS 3 - Defining AEG / GDP.
Having a positive D% avoids payments fatigue and minimises the level of arrears. Clearly, for a non-average borrower each borrower will have his/her own D% value.
CALCULATING D% The important point is to the payments becoming easier every year for say, 95% of borrowers. Or failing thatm to have this happen in most years.
That means doing some researches on a lender's mortgage book - the way in which those actual borrowers' incomes are likely to behave going forward - how much the deviations from your average income the individuals will stray. You can try doing a survey and using Standard Deviation and Mean calculations.
This may help to determine a practical minimum value for D%. For example, if 95% of borrowers' earnings are rising at a rate which is within 2% of AEG% p.a. then a value of D% which is above 2% will ease the burden of payments for that 95% of borrowers.
It is also important that this happens for borrowers during the early years. Later on the value of the debt is less and payments can be rescheduled over a longer period very easily. So a high 'D%' value in the first year can be safer than a constant 'D%' value every year.
Another safety margin can be created by allowing the total repayments period to vary. A short addition to the repayment period can make a large difference to the payments increase needed.
This is also one reason for lending over 25 years rather than over 30 years or more. An extension to 30 years can help a great deal if a borrower needs help.
Adding in the value of D% (placing the 'X' to the left of the AEG% p.a. line has the effect of increasing the initial cost 'P p.a.' of the mortgage. This first yeat payments level is called the Entry Cost of a Mortgage. Hopefully it will also be the Safe Entry Cost by the time we have done all the researches needed.
For every 1% value given to D% p.a. the entry cost P% p.a. rises by 1% p.a.
P% = C% + D% + I% - Ingram's Safe Entry Cost Equation
See PART 2 for the derivation.
SUMMARY
So far we have established the components of the Risk Management Chart, the fact that we can draw a standing loan line which slopes downwards at 45 degrees, and crosses both Axes at r%, the level of the nominal rate of interest.
This means that the vertical and horizontal sides of the triangle, formed by the standing loan line with the two axes, have equal sides.
We have also placed an AEG% (Average Earnings / Incomes Growth) line on the chart. We know that this line moves to the left and to the right as the value of AEG% p.a. (the rate of average earnings growth) changes.
The reason for calling it Average Earnings Growth is that when these studies first began there was no incomes index in the UK, only an earnings index. It may prove to be more practical to replace AEG with AIG - Average Incomes Growth because many borrowers will not have additional earnings from rentals and dividends, royalties, etc.
We have not yet found out much about that entry cost equation but it is clear that if the equation for P% is correct, a 1% rise in D% adds 1% to the entry cost. It is a very simple and neat relationship which we will be using in the management of arrears risk.
PART 2
Derivation of the Safe Entry Cost Equation
OBJECTIVE
To be safe, we want the 'X' on the chart to be to the left of this moving AEG% p.a. line to prevent payments fatigue and defaults.
And the 'X' needs to be above the, (moving), standing loan line, whose location and height in terms of P% p.a. varies with r% if the interest rate is variable.
FIG 2.1
And the 'X' needs to be above the, (moving), standing loan line, whose location and height in terms of P% p.a. varies with r% if the interest rate is variable.
FIG 2.1

Here in FIG 2.1 are three new letters:
C% = the distance of the 'X' above the standing loan line. This is a form of capital payment which ensures that the loan will be repaid. The value of C% largely determines when the debt will be fully repaid.
As time passes the loan gets smaller, the interest component of the repayment gets smaller, and C% gets larger. As more capital value is being repaid less of the payments P are used to cover the interest added.
D% = the distance of the 'X' to the left of the AEG% p.a. line as already explained. As long as D% is a positive figure, this ensures that the payments will increase more slowly than average incomes. This is called the rate of Payments Depreciation, D% p.a.
NOTE the precise definition of D%:
D% = AEG% - e% - (ii) - all are p.a.
DEFINITION
I% = r% - AEG% - (iii) as shown on the chart
or if preferred:
r% = AEG% + I% - it means that the nominal interest rate r% is the sum of these two components.
If you have been reading the economics paper, the core part of the interest rate adjustment is AEG% p.a.
The real economic part, which adds value (NAE) to the debt, is I% p.a.
Remember, if interest is added at AEG% p.a., then the total sum repaid is equal to the number of NAE borrowed in the first place.
All of these variables are p.a.
FIG 2.1 again

This third distance I%, could just as easily have been shown on the Y-axis but there is a reason for placing it on the X-axis.
I% is called the 'true' rate of interest and is defined as the marginal rate of interest above AEG% p.a:
For example, if I% = 0% it means that the interest added to the loan is equal to the rate at which average earnings / incomes are rising, AEG% p.a.
Because this is NOT the real rate of interest which is the marginal rate above a prices index, it needs a new name. Because there is no such name in the dictionary, I have called this the True rate of interest.
FIG 2.2 - Derivation of P% = C% + D% + I%
 Note that there are two small equal sided right angle triangles:
Note that there are two small equal sided right angle triangles: One with two sides of I% shown by the double headed arrows
and
One with two sides of D% again shown by double headed arrows.
Hence by adding up the vertical distances we can see that:
P% = C% + D% + I%
PART 3
Discussion of the variables
WHAT THIS EQUATIONS TELLS US
This means that ALL debt repayment schedules have these three parts, C%, D%, and I%, whether intentionally or not. It may be a Level Payments Loan, (an annuity loan), or a standing loan, or an overdraft or an ILS loan. Whatever the contract may say there is a place on the chart with a value of P% and a value of e%. Therefore P% can be divided up into these three elements.
There is no debt repayments schedule which has no value of e% or no value of P%. Since all debt repayment schedules have a value P% and a value e% they also have a value for C%, D%, and I%.
This means that any current loan repayments schedule can be converted into an ILS repayments schedule, which as explained above, may result is a rescue for both lender and borrower.
Even if e% = 0% as with Level Payments, the location of the 'X' that describes the repayments is on this chart and so P% contains a value for D% and a value for C% and a value for I%.
One interesting thing that I tested was whether the level payments equation is a special case of the general equation.
So let us put e% = 0 % in this equation. We already have:
D% = AEG% - e% - (ii)
So this means that when e% p.a. = 0% p.a. we have:
D% p.a. = AEG% p.a. - (equation x say)
Now we have: P% = C% + AEG% + I%
We also know that
I% = r% - AEG% - (iii)
which using (x) for D%, and (iii) for I% gives:
P% = C% + AEG% + r% - AEG%
So P% = C% + r%
Which is indeed the equation for an annuity mortgage with level payments. You pay capital plus interest.
CONSTANT 'LOAN: INCOME RATIOS'
I wanted to know how P% would vary as AEG% p.a. changed. There is no change in P% when AEG% varies. The entry cost is the same no matter what the rate of inflation of earnings (and everything else). So then the amount lendable is also the same for any goven income. Here's the proof:
By removing the Y-Axis we get the same equation for P% but there is no change in P% as the value of AEG% varies. We can re-draw the chart like this:
FIG 3.1 - Ingram's Risk Management Chart (Relative)
Everything is relative to AEG% p.a.
In the economics papers, AEG is like the rate at which the KFPP platform is rising. or the ship is rising as the water level changes. With all of the passengers, P%, C%, D% and I%, on board, none of them notice the tide or the pace at which the KFPP platform is rising.
People are wholly unaffected.
But of course, in the real world, not all incomes and prices rise at the same time. It is better to have a low rate of devaluation of money / price rises.
The difference between a theoretical economy in which money never falls in value and AEG% p.a. = 0% p.a. and a real economy which is financially stable, is that theroetically every cost, price, earnings, and value, rises at the same AEG% p.a. rate. In practice some of these prices (all are a form of price paid for something including the cost of hiring a person or an enterprises), do not take place on the same day. So real economies cannot be entirely financially stable. Some people get an advantage over others during the adjustment period. Otherwise, as AEG% p.a. reduces these differences also reduce and in theory at AEG% p.a. = 0% p.a. they all vanish.
What keeping pace with AEG% p.a. means is that the value of something keeps pace with everything else and the costs also keep pace. The effect of the falling value of money is neutralised.
It is the same for pension funds - they also want to be on board this ship / platform. They want to keep pace with AEG% p.a. So if they are financing the mortgages they can offer a loan at a fixed rate of I% interest with the capital then rising at AEG% p.a.
r% = AEG% p.a. + I%.
They just need to see that I% is positive and they will sit there on board the ship collecting I% interest whilst adding AEG% interest to the capital debt. The caital lent will keep pace with NAE and the interest can be used to pay for administrtion and risk.
If AEG% reaches zero, if money has a constant value, (not constant purchasing power which is different), then I% = r% - the nominal rate of interest. Remember:
r% = AEG% + I% by definition.
What has happened with this safe entry cost equation is that incomes inflation has been taken out of consideration. Everything works the same as if AEG% p.a. was zero. C%, D%, and I% are not altered. P% is the same. The safe entry cost for a loan is the same. The amount which a person can afford to borrow is the same because the entry cost is the same.
What if AEG% p.a. goes negative?
Nothing changes. The relative chart is the same. The 'ship' goes downwards. Everything is on board. The repayment term, being governed by C% is the same. As always, D% will be unchanged and positive. The payments will be falling at D% faster than national average earnings are falling. An economic depression with not harm the borrowers on this side of their expediture. Lenders ill have fewer problems with arrears.
Lets us look at some examples of ILS Loans with various rates of AEG% p.a. Here, incomes are not rising but the payments are falling. The nominal rate of interest is low at 3% but that is not low for I% based on past data for three nations studied. It is average in al three nations over the period before we had super-low rates of interest in the erly 2000s and asset prices inflated and, and, and everything went wrong.
FIG 3.2 - ILS Mortgage with AEG% = 0% I = 3%
Note that the payments fall every year and that the '% of income' used every year falls to 11.26% in the final year.
CONVENTION USED
NOTE: when we say '% of income' we are taking a percentage of a standard income which is defined as one which changes at the rate of AEG% p.a.
The borrower's income could start out as 1 NAE - one National Average Earnings / Income (1 NAI), and so the amount borrowed would be 3.55 NAE in this example. See bottom line, first column where it says 3.55 times income as the size of the loan.
This means that all of the '% of income' data is a percentage of 1 NAE. In this example the total cost would have been 4.80 NAE as shown in the 'Total in Yrs of Income' cell.
This is how that payments schedule looks:
FIG 3.2a - AEG% = 0% I% = 3% BARS for '% of Income' as cost.
Again, the bars represent the falling number of NAE being repaid. If the borrower's income is more than 1 NAE then the loan is that much larger and the bars are that much higher but the shape of the bar chart is the same.
Now if we examine what happens if AEG% is high, at 9% p.a. we get this:
FIG 3.3 AEG% = 9% I% = 3% as before
The same pattern appears in the final column. Compare the numbers with the previous tabulation above. And the amount lent is about the same as before with the entry cost also about the same as before.
NOTE: If the table did not use annual intervals but daily intervals to apply interest and payments it is thought that the amount borrowed would not be different as AEG% p.a. changes. That is a challenge for some clever reader to prove.
The net cost in terms of total number of years of the borrower's income paid as interest is 32.7% interest on the loan, being the total cost of 4.55 years' income, less the amount of 3.43 years' income originally borrowed. This is similar to the previous example.
There are slight differences in the figures, which I must ask an actuary to explain! See the note above.
But broadly speaking nothing much has changed. Unless, that is, you look at the money data which is totally different. The net cost is now 317% of what was borrowed whereas previously it was 35.2%. Counting the money cost is highly misleading.
If we try the same tabulation with D% = AEG% = 4% and I% = 3% we get the Level Payments Model with r% = AEG% + I% = 7% as before. This is because in all of my illustrations I have set D% at 4% p.a. If AEG% = D% we have the level payments model.
FIG 3.4 - This is another ILS Model but it could also be the Level Payments Model at AEG% = D% = 4% and I% = 3% again. That is because in the LP model AEG% = D% and e% = AEG% - D% = 0% in that case.
Check out all the figures in the bottowm row. Only the money figures look much different.
The BAR charts of FIG 3.2a would all look very similar for all of the above examples. If you looked only at the bar charts, as long as D% = 4% and I% = 3% in every chart, you would not know the value of AEG% p.a. The bar charts all look the same. They show the % of income figures.
FIG 3.5 - Incomes falling
The standing loan can be extended to the left of the Y-axis too.
The value of P% is not any higher just because the 'X' is to the left of the Y-axis because this condition lowers the value of r% - unless there is something distorting interest rates! We will be looking at the behaviour of interest rates.
If readers look again at Table 3.2 this illustrates this chart with the 'X' exactly where it is here.
PART 4
FROM THIS POINT ONWARD EDITING IS IN PROGRESS
FROM THIS POINT ONWARD EDITING IS IN PROGRESS
The key to note is that I% p.a. is the rate at which NAE is added to the mortgage debt, L, expressed in units of NAE.
I% provides a positive true rate of return / interest to the lender / investor.
Any higher than that indicated by Siegel's Constant and the level of demand will generally bring the true rate of interest back down. Besides that, the higher the value of I% the fewer borrowers there will be wanting to borrow.
Here are some interesting case studies of how the money looks in various scenarios:
to be continued shortly
=============================
What happens if D% = 0%?
If we are to compare the arrears risk of various mortgage repayment models we have to look at the likely behaviour of D% as we endeavour to keep the repayments on schedule without interfering with either C% or P%.
LOOKING FOR SAFE MORTGAGES
/ OTHER DEBT STRUCTURES
Given that D% needs to be positive, we can decide which debt repayments models are safe and which are not. Those that have no control over D% are not safe - at least not for people. A government can mange with D% = 0% without getting payments fatigue because tax revenues go on and on and should never depart too far from AEG% p.a. even in a recession.
Over short periods there is likely to be a strong relationship between AEG% p.a. and the rate of change of Nominal GDP, but if a large part of the working population jumps ship / emigrates, or if unemployment rises significantly, there will be some divergence.
Since the value of D% is the distance of the 'X' from the AEG% p.a. line, it follows that if e% = 0%, as it is with a fixed interest mortgage or a fixed interest government bond, then since the AEG% p.a. line is always on the move, the value of D% p.a. is always on the move.
In fact, AEG% p.a. can go negative as it has done in some European countries recently.
The effect on this of I% can be very nasty. Remember:
I% = r% - AEG% - (iii)
For example, if r% = 3% nominal interest
AEG% = -5% p.a.
You get I% = 8% p.a.
That is 8% of the income borrowed added to the debt by the true rate of interest. A debt of 4 times income then rises at 4 x 8% = 32% of income p.a.

The mortgage schedule begins to look like this:
This also affects an investment in a government bond hugely during a slow down or a recession. Below is a graph showing how that has affected the return on US treasuries on a year by year basis since 1980 when inflation was high and since when it has fallen to almost zero. The effect is the same:
Try r% = 20% and then AEG% falls from 25% to 11%. You get I% = 20% - 25% at first = -5%
But then this becomes
I% = 20% - 11% as inflation comes down = 9%.
This is like what happened to USA Government Bonds and the result was this graph:
| Source: Morgan Stanley Research c/o Money Game Chart of the day. Figures adjusted by Edward for AEG to reveal the true rates of return. |
As can be seen the return on USA AAA rated bonds reached 25% one year and averaged something like the trend-line shown. This average reflects the cost to USA tax payers of using fixed interest bonds over that period.
This additional GDP added to the total government debt is probably enough compounded up to explain most of the rise in USA government debt since that time! For example, 5% p.a. compounded over 25 years comes to a 3.6 fold increase in the original number of GDP owed in 1980 if no repayments were made. Certainly 9% true interest would not have been paid. Some part of it maybe would. Even paying 5% is steep.
THE DANGER OF A BOND CRISIS
Now that interest rates are virtually zero there is a significant danger that the value of these bonds may collapse when Quantitative easing is reduced and interest rates rise. This can produce another world crisis of enormous proportions and is the worry of one Andy Haldane at the Bank of England as expressed in The Guardian newspaper recently (before this weekend of 15th June 2013). His remarks may be enough to cause another panic - we will see.
The interest rate sensitivity of mortgage finance is also very great and it is this which accounts for the rise and fall of property prices and which can also undermine the whole economy.
In both cases we need to reform the debt structures.
IN SUMMARY
The cost-to-income of the fixed interest mortgages or even the low interest rate mortgages rises every year if average incomes are falling. The same applies to government fixed interest rate debt / bonds. The cost rises every year. This is not safe, and it leaves investors not knowing what kind of I% they will get on their investments. If a recovery comes then I% can even go negative. So this arrangement is not safe for borrowers or for investors / lenders.
Given the amount of wealth invested in both housing and government bond sectors this is very distressing to the performance of the whole economy.
What we are looking for is a repayments model which looks something like the sketch already presented twice now:
Repayments follow a more 'normal' rental type model, rising with incomes but not quite as fast.
Looking at the equation:
P% = C% + D% + I%
we see that adding in D% to get this slope adds to the value of P% - the initial cost of the repayments.
Putting D% p.a. = 4% adds 4% to P%.

Such a repayments model might look like this if I% had been fixed at 3%. (I% can be fixed by offering fixed true rate wealth bonds to investors).
The downwards slope means that D% p.a. is positive. In this illustration the payments start at 30% of income and reduce at 4% p.a. to reach around 11% at the end of 25 years. The slope is the value of D% and so it is based on the AEG% p.a. index of incomes, not individual incomes. But if the slope is steep enough all borrowers within reason should be able to cope with the repayments.
In practice the straight sloping line should be curved, but it helps to make the point when I do not show the curves of compounding.
As already pointed out there is a BIG problem with Level Payments and Fixed Interest
Let's do a short revision course.Originally I wrote the following script about the fixed interest mortgage model - it goes over what I just wrote above, but in a different way:
Given that, by definition:
D% = AEG% - e% - (ii)
we can see that fixing e% = 0% can lead to problems when AEG% is close to zero because if e% = 0% for level fixed payments and AEG% = 0%, then D% = 0%.
Example for austerity:
AEG% = -2% and e% = 0% gives:
D% = - 2% - 0% = -2%
So as already mentioned above, the payments are costing a 2% higher proportion of average income every year. Like this:
Here D% p.a. is negative so the slope is up instead of down and payments are rising relative to average income every year.
What is worse is that the value of I% also rises. I% governs the cost-to-income that the borrower has to repay. I% adds wealth to the wealth debt already owed. Suppose that the lender offered a fixed rate of nominal interest with r% = 3% but then AEG% fell to -2%. We know that:
I% = r% - AEG% - (ii)
So I% = 3% - (-2%) = 5%.
This is more costly to the borrower than raising equity capital. For lenders 5% above AEG% p.a. pays better than investing in equities and property. I am assuming the equities investment data on that for the USA / UK applies here.
For other nations lenders need to do more researches to reach their figures. But normally one would expect a high rate of return that out-performs long term investments in equities and property to lead to major problems for prospective new borrowers and a flood of money on the books of lenders which they would not be able to lend.
As already noted, normally the value of I% (net of lending costs and taxation) should not exceed the rate of return on such other investments but it should also be above zero to limit the demand for borrowing.
PREVENTING THE NEXT CRISIS
Imagine that a UK lender was to offer a 10 year fixed true interest rate of 5% p.a. The number of older people wanting a safe investment that performed that well would be very high. It would provide a very safe annuity. I have listed a whole range of uses for this kind of bond on this page called NEW FINANCIAL PRODUCTS RESULTING.
As soon as these kinds of wealth bonds become available there will be a major clamour for such products because nothing sells better than risk free (to wealth) investments. But to make that happen in time to prevent Andy Haldane's feared crisis there needs to be a commission of enquiry set up and an IMPLEMENTATION programme developed as outlined on that same blog.
There we are discussing the replacement of fixed interest bonds with wealth bonds in a very different environment of low true interest rates - but safe wealth will attract a massive demand at an rate of true interest in the environment that currently prevails. Doing so will safeguard the banks' balance sheets. Offering the replacement wealth bonds at a discounted price would cut the government's debt.
Investors face the alternative of imploding bond values as interest rates rise, so a discounted rate may well be popular.
Going back now to looking at the upper boundary for I% in more normal economies:
The number of borrowers wanting to borrow at a 5% level of I% would be much fewer because the slope for D% p.a. would reduce to 2% p.a. compared to the illustration above:
P% = C% (about the same) + D% (2% less = 2%) + I% (2% more).
By keeping C% the same the total repayment period would remain close to 25 years. To do that D% has to drop to compensate for the higher level of I%.
Then we get this:

The slope is 2% less and the total cost is a lot more.
I will come back to this a bit later with more detail.
CONCLUSIONS
1. A fixed interest mortgage does not look viable when AEG% p.a. is falling. For another example if AEG% = 10% and r% = 13% fixed, what happens when AEG% p.a. falls to 5%?
I% = 3% at first but then rises to 8%.
This is similar to what happened to the USA government bonds in the 1980s. See above. It meant that AAA rated bonds were yielding far more than share investments ever did over the longer term.
2. If we look at the main equation:
P% = C% + D% + I%
We can see that a rising level of I% requires a lower value of D% if P% and C% and the total repayment term are to remain the same.
In fact if I% increases by 1% the D% must decrease by 1% or the mortgage will go off schedule as C% adjusts instead. Or P% will rise - taking us back to the same old problems that we are having with variable interest rate mortgages now.
For the moment let us not look at variable rates. Above we are looking at fixed true rates. So if the fixed true rate on offer to lenders out there in the market for say 10 year bonds or longer, rises by 1% then D% will fall by 1%.
SUMMARY SO FAR AND MORE
I named the main equation P% = C% + D% + I%
Ingram's Safe Entry Cost Equation because it can be used for setting the entry cost (the initial value of P%) and because I was unable to patent it I attached my own name to it.
Interestingly the value of P% does not depend upon the value of either r% or AEG%. It depends on I% which is the difference - the marginal rate at which NAE gets added to the debt.
I% = r% - AEG%
So the rate of inflation, or AEG% p.a., in a nation should not affect the amount that can be lent safely - by much.
The most important difference would be the variability of incomes growth between different members of the working population. If this gets too big then it needs a larger D% to accommodate it.
In fact this is a general equation which can be applied at any time to any form of regular payment debt. It takes the basic elements of Payments Depreciation, D% p.a. Capital repayments C% p.a., and wealth addition (I% p.a.) and adds them together to get the cost of the payments P% p.a.
P% = C% + D% + I% - all are p.a. - (i)
PART 5
A DETAILED LOOK AT TRUE INTEREST I%
AND WEALTH
First, some more revision...REMEMBER:
I% is not the nominal rate of interest 'r%'; it is the marginal rate above AEG% p.a. I called this the True rate of interest.
I% = r% - AEG% - (ii)
ABOUT TRUE INTEREST I%
When the interest rate = AEG%, say 4% p.a. and incomes are rising at the same 4% p.a. the amount owed at the end of the year is 104 per 100 debt.
But if incomes also rose by 4% the debt / income ratio is no higher:
If income was 100 at the start of the year it will also be 104 by the end of the year.
So a year's income was borrowed and even without making any repayments at all, the loan will still be one year's income at the end of the year.
Only the excess interest above AEG% p.a. increases that ratio. Only that excess (marginal / true) interest adds to the cost of borrowing for a person on average income increases.
If r% = 10% then the loan will be 110 at the end of the year and if incomes are rising by only 4% p.a. then income will be 6% less at 104.
I% = 6%
At this rate the income owed increases by 6% p.a. compared to the income borrowed. But we are talking here of average incomes...
BORROWERS V INVESTORS
New script
What the borrower sees and what the investor / lender sees are not the same.
We can think of borrowers as not all getting average income increases. For those with incomes growing less quickly the cost-to-income will be higher. For those with incomes growing more quickly the cost-to-income will be lower.
For the investor looking to lend money and to preserve the years of income that has been saved and lent, they want to keep pace with, or do better than, the average / the index, much as they may expect to do over the long term with equities or property. All have a loose link to AEG% p.a. the aggregate demand baseline of economies.
However, market forces, or counter-inflation policy, will determine the interest rate unless it has been distorted by something.
DEFINING WEALTH
So let us define wealth as the number of years' income that has been lent.
This definition of wealth is useful because when I% is positive it moves wealth from the 'average borrower' to the investor. In this sense, wealth can be defined in units of National Average Earnings, NAE.
NAE is the part of the national income that a person has earned as income or profits, or has been given, or acquired in some way.
If that part of National Income is not preserved when it is invested, some other person or entity will spend the part that has been lost.
For example, look at this spreadsheet which is produced by the EXCEL sheet mentioned earlier as being for sale:
FIG XX - Negative true interest moves wealth from lender to borrower
The wealth lent was 4.23 years' income. The wealth repaid is found by adding up the '% of income' numbers which comes to 320% or 3.20 years' income as shown. This is 1.03 years' income less wealth / income than was borrowed, as shown. The net cost of borrowing is -24.3%.
This income (wealth) has not been lost. The borrower first spent the income (NAE) that he/she borrowed / was lent, and then repaid less NAE so he/she was able to spend the income / wealth (NAE) saved on something else. The table does not show the NAE but one could try this: assume that the borrower was on average income and then the table does show NAE. 4.23 NAE was borrowed and 3.20 NAE was repaid.
Wealth did not vanish - it moved. 1.03 NAE moved from the lender to the borrower.
The same applies if I% is positive - wealth moves but this time in the other direction.
TAX DISTORTION
If we look at the MONEY repaid in the above illustration it looks like a 77.4% profit. That gets taxed - haha! Some joke. Some distortion.
Distortions all cost the economy and the social fabric something, so we will need to look into this and see how we can sort it out without messing anything up. It can be done.
In America they give tax relief on the interest paid! Giving tax relief on AEG% of the interest is a variable rate gift and another distortion. It is not needed. The net result of both tax regimes combined (taxation of all interest and tax relief on all interest), is to tax saved wealth and give it to borrowers. It reduces the ability of lenders to keep interest rates down. The main effect is to increase administration costs.
In reality, in the above scenario (see the table again), the borrower spends the 4.23 years' income right away and only has to repay 3.2 years' income leaving him/her free to spend the remainder at will on whatever is wished.
A year's spending power has left the lender and moved to the borrower.
Imagine if the borrower's property has risen at the same rate as AEG% p.a. That is quite possible, even probable. He/she will do very well.
He/she borrows at AEG% - 3% p.a. and his property rises in value at AEG% p.a. and attracts rental on top.
TRUE COST DEFINED
If I% is positive, we now can see that the cost-to-wealth of the repayments, as opposed to the cost-to-income of a particular borrower, is the true cost (actual cost to wealth). The true cost is not the cost to the income of a particular borrower. It is the wealth that has been borrowed plus the overall cost of the marginal interest rate I% which has increased the wealth owed and added to the wealth of the lender.
TWO MEASUREMENTS
In all my spreadsheets readers will find two cost figures:
There is the money cost and
There is the wealth cost, or the 'true cost' as I call it. This is the number of year's income that it takes to repay if the borrower's income rises as fast as average. True cost can also be expressed in NAE. For governments it can be expressed as a fraction or a percent of GDP.
The two figures, money cost and true cost usually look very different.
When inflation is high and interest rates are high the cost to money can be very high indeed, yet at the same time the cost to income can be very low or even negative.
This means that the figures offered to the public can be very misleading.
REAL INTEREST IS NOT ENOUGH
Even if the figures are adjusted for prices inflation they can be very misleading:

Here the nominal interest rate is 12% and prices inflation is 7% so the real interest rate is 5%:
12% - 7% = 5% real interest.
But the true interest rate is only 2%:
12% - 10% (AEG%) = 2%
If the nominal interest rate had been 8% then the real interest rate would have been +1%:
8% - 7% inflation = +1% real interest
but the true interest rate (I%) would have been -2%
8% - 10%(AEG%) = -2%
8% interest means that a loan of 100 becomes 108 at year's end
But incomes would be 110 by year's end.
So now we see that the average borrower will not need to repay the whole year's income that was borrowed. 2% less wealth will need to be repaid than was borrowed just in that one year. Yet the real rate of interest was +1%. Real interest does not protect wealth.
So an index-linked investment which is linked to prices does not protect wealth.
You do NOT find that in your text books!
MISSING TABLE
I compiled a table to show how much 'wealth profit' an investor can get from buying a fixed true rate bond at various rates of interest and I included the cost to a borrower over a 25 year term from borrowing at the same rates of interest. I will add this table when I locate it. I gave an example of 5% true interest increasing wealth by 3.6 fold though. So it can be seen that quite small amounts of true interest are very attractive to older people seeking security.
THAT EUREKA THING
NOW we see why it was so important to introduce I% into the main equation. I% is the rate of wealth transfer. A high I% is a serious factor in any debt repayments schedule. Wealth as measured / added by I% is a real and tangible thing that has never been declared in our text books.
And it brings to the fore the importance of AEG% as a baseline for everything in the economy - all forms of investment are propelled by AEG% p.a. - by aggregate demand and how fast it changes.
If we adjust all prices and repayment costs for AEG% p.a. everything will be seen as if there was no AEG% p.a. Everything is relative to AEG% p.a. Only the excess I% adds a cost or a benefit. Only I% moves wealth.
SUMMARY
True interest is a key component of the economy. It is responsible for wealth transfer on a massive scale, even when it is not very high.
The text books are not telling it as it is when they write of real interest rates. Real interest rates do not preserve wealth.
A true rate of interest of zero incorporates the real rate of economic growth (approximately) and is a great selling point to raise funds for lenders - and for governments. Yet it costs the borrowing house buyer or government no actual wealth.
Eureka! - What have we been thinking all this time?
PART 6
TESTING APPLICATIONS OF THE EQUATION
The data that I have for the UK shows that the true interest averaged +3% on home loans from 1970 to 2002. I got a similar figure for South Africa and I used this 3% figure to forecast by how much the Fed might need to raise interest rates in 2006 / 8. My forecast was almost exactly in line with what was actually targeted. It was just that to target such a 4.5% raise in interest rates implied a 58% increase in the cost of variable rate prime mortgage payments!
I wrote this page on Finding the Mid-Cycle Rate of Interest as a result of that calculation / observation.
Clearly, you cannot lend a whole lot more just because, temporarily, interest rates have fallen, no matter how far they have fallen.
So I have used 3% true interest as a baseline for my studies and simulations - the assumed average rate. Readers can experiment with other average rates and I have done that too. My spreadsheets are available for sale. So given that baseline:
Given that P% = C% + D% + I%
We can put in some figures:
P% = 1.5% + 4% + 3% = 8.5% p.a.
This is approximately the data that represents a 25 year mortgage repaid with 4% p.a. Payments Depreciation and at 3% true interest.
It creates a mortgage of 3.5 times income.
This is the original 3.5 times income mortgage that I illustrated above where the payments fell at 4% p.a. and which cost 30% of income falling to around 11% of income (shaded area) when I% = 3%.
If the true interest rate I% is 5% this means that D% now has to reduce D% from 4% p.a. to 2% p.a. because I% is 2% higher:
P% = 1.5% + 2% + 5% = 8.5% as before - so we still have a 3.5 times income mortgage because the entry cost is still the same.
 We cannot reduce C% because that will cause the loan to take longer to repay.
We cannot reduce C% because that will cause the loan to take longer to repay.We do not want to increase P%, because that will hit collateral security / house prices, (but we can lean that way), so what is left is D%. This value must fall by 2% if I% rises by 2% as shown in this sketch.
Tests show that if the current true rate of interest is +11% or -7% (two extreme figures taken from South African data), the entry cost can still be set close to this mid-cycle figure because such extremes reverse and go the opposite way. The true rate still averages about the same figure.
I will add some back-testing data on a new page when I have time. It is already there for customers on the spreadsheet.
PART 7
From here on readers will find extracts from the earlier paper which is still to be found on the next blog page - MATHS 1
The Risk Management Chart and the standing loan line also works when e% is negative and payments are falling.
FIG 1.4 – Payments falling - but with the 'X' above the standing loan line, the debt is falling faster than the payments. If the 'X' was on the standing loan line both the payments 'P' and the loan 'L' would be falling at the same pace. But neither of them would reach zero. Ever.
So here, at the tip of the arrow, the standing loan line shows that the payments are falling (e% = -4% p.a say), but the payments are so high that the loan size is also falling by 4% p.a. Neither 'L' nor 'P' ever reach zero. Every year 96% of what was there the previous year remains as the balance owed at the end of the current year.
When we place the ‘X’ above the standing loan line as shown and with AEG% p.a. = 0% as shown in FIG 1.4, with r% = 3%, the loan will fall faster than the payments and the mortgage will be repaid on schedule. See FIG 1.5 below.
When we place the ‘X’ above the standing loan line as shown and with AEG% p.a. = 0% as shown in FIG 1.4, with r% = 3%, the loan will fall faster than the payments and the mortgage will be repaid on schedule. See FIG 1.5 below.
FIG 1.5 – Payments Falling with e% = -4% p.a. and AEG% p.a. = 0% (Average incomes not rising). D% = AEG% = 4% p.a.
The good news is that in this case, with incomes not rising, it is likely that the economy is in recession, and / or the rate of interest is very low. So the standing loan line is much lower as shown in FIG 1.5. But to achieve this level of D%, P% may be almost the same 8.5% p.a. as before the recession.
SIZE OF MORTGAGE
At this level of P% = 8.5%, the amount that can be lent on 30% of income in repayments is 3.5 years' income. You can use gross income or net income as long as you use the same figure for both. Lenders decide how much of the gross income should be affordable and whether or not 30% is the right figure.
TOTAL COST TO INCOME
If you add up all of the '% of incomes' you get the total cost-to-income of the repayments which is shown as 4.8 years' income, or 1.25 years' income more than was borrowed, which is 35.2% more than was borrowed as shown.
If we put P% = 8.5% when AEG% p.a. = 4% and the true interest rate is still 3% as in the above example, the amount lent will still be 3.5 years' income and the repayments will cost 34.9% more than the income borrowed, (almost the same figure).
A true interest rate of 3% is the long term average rate of true interest (my estimate) for the UK. Notice that the amount lent in both of these examples is 3.5 years' income. As stated earlier, the value of P% does not depend on the nominal rate of interest. It is a function of the true rate of interest I%:
P% = C% + D% + I%
COMMENT
Did you know that the IMF's Country Report 2012 said that house prices are now averaging 4.5 years' income whereas long term in the UK they have averaged 3.5 years' income? That was when 3.5 years' income mortgages were common. Now, with interest rates being held very low, they are lending more but they are not making enough provision for interest rates to rise. See FIG 1.6
HAZARD OF ECONOMIC RECOVERY
FIG 1.6 - Look where the lower 'X' is placed. Note how when interest rates rise the standing loan line will rise forcing the 'X' to jump up the Y-Axis adding over 30% (maybe 50%) to the entry cost of new mortgages and hitting both property prices and variable rate mortgages hard.
The AEG% p.a. line will move to the right.
SIZE OF MORTGAGE
At this level of P% = 8.5%, the amount that can be lent on 30% of income in repayments is 3.5 years' income. You can use gross income or net income as long as you use the same figure for both. Lenders decide how much of the gross income should be affordable and whether or not 30% is the right figure.
TOTAL COST TO INCOME
If you add up all of the '% of incomes' you get the total cost-to-income of the repayments which is shown as 4.8 years' income, or 1.25 years' income more than was borrowed, which is 35.2% more than was borrowed as shown.
If we put P% = 8.5% when AEG% p.a. = 4% and the true interest rate is still 3% as in the above example, the amount lent will still be 3.5 years' income and the repayments will cost 34.9% more than the income borrowed, (almost the same figure).
A true interest rate of 3% is the long term average rate of true interest (my estimate) for the UK. Notice that the amount lent in both of these examples is 3.5 years' income. As stated earlier, the value of P% does not depend on the nominal rate of interest. It is a function of the true rate of interest I%:
P% = C% + D% + I%
COMMENT
Did you know that the IMF's Country Report 2012 said that house prices are now averaging 4.5 years' income whereas long term in the UK they have averaged 3.5 years' income? That was when 3.5 years' income mortgages were common. Now, with interest rates being held very low, they are lending more but they are not making enough provision for interest rates to rise. See FIG 1.6
HAZARD OF ECONOMIC RECOVERY
FIG 1.6 - Look where the lower 'X' is placed. Note how when interest rates rise the standing loan line will rise forcing the 'X' to jump up the Y-Axis adding over 30% (maybe 50%) to the entry cost of new mortgages and hitting both property prices and variable rate mortgages hard.
The AEG% p.a. line will move to the right.
To avoid or postpone this problem is why keeping interest rates down is essential to economic recovery - so they say. If they allow interest rates to rise naturally, the cost of borrowing will jump sky high and property values will drop. The banks will be threatened again, not just by property prices tumbling and arrears and repossessions rising, but also their reserves invested in fixed interest bonds will also take a beating. But they have not seen this chart and the solution to the problem which is to move the 'X' to the right. And they have not read the next page on government bonds.
When the 'X' gets moved to the right as a rescue operation for the Level Payments Model, this is known as the ILS HYBRID Mortgage Model. It starts as a Level Payments Model but gets rescued by the ILS move to the right!.
When the 'X' gets moved to the right as a rescue operation for the Level Payments Model, this is known as the ILS HYBRID Mortgage Model. It starts as a Level Payments Model but gets rescued by the ILS move to the right!.
If you would like to use the spreadsheets that I use to produce all of these illustrations, including a full range of bar charts and spreadsheets, and the ability to input historic data as you wish, you may buy a copy. This is really the only way to thoroughly understand the subject and to test the proposed debt models. Send me an email to:
The cost to a full time student is very low. The cost to an institution is high - you may not share the software with others. One copy per computer.
GENERAL APPLICATION
OTHER MORTGAGE MODELS
In order to convert from one style of debt repayment model to another you just need to change the way in which you are managing the values C% and D%.
EXAMPLES If r% and P are both index-linked to a prices or an incomes index then you have a problem. You are not managing D%.
If the payments are linked to the wages index as in Turkey, then D% = 0%.
If payments are linked to prices then D% is approximately the rate of real economic growth, which can turn negative.
Most index-linked models (all that I know of) index-link both the payments P (e% p.a.) as well as the interest rate r%. As stated, this means a loss of control over D%. In fact, the only models that mange D% appropriately are these ILS Models, based on this mathematics.
THE SAFEST MORTGAGE OF ALL
Sorry - this is a bit repetitive but sometimes repetition helps...
There is one ILS Model in which I% is fixed by agreement with the lender / investors who also get a fixed I% p.a. reduced by costs. In such a case, as the lender adjusts the value of r% as AEG% varies so as to keep I% constant.
I% = r% - AEG% = constant
This gives a very safe:
P% = C% + fixed D% + fixed I% - remember that P% and C% are not fixed: every year as capital is repaid they both increase by the about the same small (at first) %.
Eventually they both exceed 100% and the small remaining debt is paid off.
This is fixed I% Defined Cost Mortgage is VERY safe because D% is fixed no matter what is happening to r% or AEG%. The fixed I% provides the lender with a positive and guaranteed return on wealth which can be passed on to the savers / investors. There is little risk of arrears because D% is fixed.
DODGING BASEL III issues
A lender can even find investors and match them to individual borrowers, taking no risk themselves. Or lenders can set up a unit trust (Mutual Fund) for deposits and lend those funds, again without taking any risk themselves. The lender is then just an agency of the unit trust fund.
EXAMPLES If r% and P are both index-linked to a prices or an incomes index then you have a problem. You are not managing D%.
If the payments are linked to the wages index as in Turkey, then D% = 0%.
If payments are linked to prices then D% is approximately the rate of real economic growth, which can turn negative.
Most index-linked models (all that I know of) index-link both the payments P (e% p.a.) as well as the interest rate r%. As stated, this means a loss of control over D%. In fact, the only models that mange D% appropriately are these ILS Models, based on this mathematics.
THE SAFEST MORTGAGE OF ALL
Sorry - this is a bit repetitive but sometimes repetition helps...
There is one ILS Model in which I% is fixed by agreement with the lender / investors who also get a fixed I% p.a. reduced by costs. In such a case, as the lender adjusts the value of r% as AEG% varies so as to keep I% constant.
I% = r% - AEG% = constant
This gives a very safe:
P% = C% + fixed D% + fixed I% - remember that P% and C% are not fixed: every year as capital is repaid they both increase by the about the same small (at first) %.
Eventually they both exceed 100% and the small remaining debt is paid off.
This is fixed I% Defined Cost Mortgage is VERY safe because D% is fixed no matter what is happening to r% or AEG%. The fixed I% provides the lender with a positive and guaranteed return on wealth which can be passed on to the savers / investors. There is little risk of arrears because D% is fixed.
DODGING BASEL III issues
A lender can even find investors and match them to individual borrowers, taking no risk themselves. Or lenders can set up a unit trust (Mutual Fund) for deposits and lend those funds, again without taking any risk themselves. The lender is then just an agency of the unit trust fund.
-----------------------------
Legal frameworks willing, any mortgage can be converted to any other kind of mortgage at any time.
P% = C% + D% + I%
The difference is just a matter of how, and if, the values on the right hand side are managed.
-------------------------------------
Take a break!
Next Session
MANAGING THE ARREARS RISK
Now we are going to look at variable rate ILS Mortgages. Variable rates can be cheaper because they tend to be funded by 'hot' money that is in the form of short term, fast access deposits upon which little or no interest is paid.
If interest is paid then rates adjust to changing conditions and the 'market rate' is established. When one has a fixed rate, the market rate can go higher or lower and this presents a 'market rate risk' to the fixed rate investor - the risk of being out of line and losing out as a result. For this reason investors like to add a bit of interest to be on the safe side of that risk.
With variable rates, however, the lending / borrowing risk of payments getting out of control depends upon how high the value of C% and D% are at outset and what is likely to happen to the value of I% over time.
If interest is paid then rates adjust to changing conditions and the 'market rate' is established. When one has a fixed rate, the market rate can go higher or lower and this presents a 'market rate risk' to the fixed rate investor - the risk of being out of line and losing out as a result. For this reason investors like to add a bit of interest to be on the safe side of that risk.
With variable rates, however, the lending / borrowing risk of payments getting out of control depends upon how high the value of C% and D% are at outset and what is likely to happen to the value of I% over time.
Remember the equation:
P% = C% + D% + I%
If I% is constant then over time the outstanding repayment period shortens every year because the ratio P/L rises - the loan reduces and the payments P remain the same. This means that C% rises and P% rises every year if the mortgage is to be repaid on time.
P% = P / L x 100%
But if I% is not a constant then, unless some adjustment is made to D%, that rising P% and C% pattern gets disturbed.
One could re-write the equation this way:
P% = F% + I%
where F% = C% + D%.
So if I% rises then F% has to fall to keep P% on course.
But in practice we would not want to disturb C% on its steady upwards path, needed to keep the repayment term on schedule. The shorter the remaining years to pay, N, the higher the value of C% has to climb. So that leaves us with a falling F% when I% rises but only the D% part of F% may be allowed to fall:
This means that in a perfect world, D% has to be large enough to stay positive when I% rises.
But in practice we would not want to disturb C% on its steady upwards path, needed to keep the repayment term on schedule. The shorter the remaining years to pay, N, the higher the value of C% has to climb. So that leaves us with a falling F% when I% rises but only the D% part of F% may be allowed to fall:
This means that in a perfect world, D% has to be large enough to stay positive when I% rises.
HOW TO SET THE SAFE ENTRY COST
SETTING I% FOR VARIABLE INTEREST RATES
The key to creating a safe variable rate mortgage, or even a safe fixed true interest rate mortgage, lies in managing D%. For this reason, the initial value of I% used to calculate a safe value for P% will not be the current value of I%.
We can modify my Safe Entry Cost Equation:
P% = C% + D% + (I% + K%)
We will not use the current value of I%, but instead we will add K% to that - K% being the amount needed to increase or reduce the current value of I% so as to make it approximately equal to the median value of I% over a cycle.
In other words, I% + K% = the median value of I%. The reason for this follows below.
NOTE ON MEDIAN VALUE
It may be better to call this 'median' value the clearing value of I%. That is the value which applies to mortgage finance when the cost of borrowing / the cost of money in the economy is such as to hold inflation steady. Aggregate demand for money is comprised of numerous arrangements from overdrafts through business loans and mortgages to government debt. The median value is the value of interest rates at which the overall demand for money is not leading to an inflationary increase in the supply of money / credit.
There is no clear way to define this figure so I have simply taken a few studies of past rates and concluded that for the developed economies it is close to 3% for mortgage finance, this being the average true rate over long periods before rates were distorted downwards at the start of this century.
The back testing done (to be added to later pages) seems to show that this method of finding the entry cost P% is workable for variable rate mortgages. In the event of a mistake being made the worst that will happen is that P% has to be raised or the repayment period extended, which is what we were trying to avoid because that is the problem we have currently with variable rate mortgages.
We can modify my Safe Entry Cost Equation:
P% = C% + D% + (I% + K%)
We will not use the current value of I%, but instead we will add K% to that - K% being the amount needed to increase or reduce the current value of I% so as to make it approximately equal to the median value of I% over a cycle.
In other words, I% + K% = the median value of I%. The reason for this follows below.
NOTE ON MEDIAN VALUE
It may be better to call this 'median' value the clearing value of I%. That is the value which applies to mortgage finance when the cost of borrowing / the cost of money in the economy is such as to hold inflation steady. Aggregate demand for money is comprised of numerous arrangements from overdrafts through business loans and mortgages to government debt. The median value is the value of interest rates at which the overall demand for money is not leading to an inflationary increase in the supply of money / credit.
There is no clear way to define this figure so I have simply taken a few studies of past rates and concluded that for the developed economies it is close to 3% for mortgage finance, this being the average true rate over long periods before rates were distorted downwards at the start of this century.
The back testing done (to be added to later pages) seems to show that this method of finding the entry cost P% is workable for variable rate mortgages. In the event of a mistake being made the worst that will happen is that P% has to be raised or the repayment period extended, which is what we were trying to avoid because that is the problem we have currently with variable rate mortgages.
In practice, with the way that so many things are currently distorting interest rates we know that I% can be down at -7% or up at +11%.
But we also know that the further it departs from the median value or the value that should balance the supply of funds to lend with the demand for them, which appears to be around 3% for the UK for example, the faster it will return to the median value and probably overshoot in the opposite direction.
But we also know that the further it departs from the median value or the value that should balance the supply of funds to lend with the demand for them, which appears to be around 3% for the UK for example, the faster it will return to the median value and probably overshoot in the opposite direction.
Past data shows that this is not a big worry for lenders. They can smooth this volatility out by not adjusting D% proportionately, but instead allowing the projected value of N to fluctuate around the target value as C% rises and falls, C% even going negative at times.
Alternatively, lenders can observe that a one year spike of 11% in I% would take D% to -7% (say) making the cost of repayments rise by 7% more than incomes are rising. This is less than the worst case result for a Level Payments Mortgage after a 1% interest rate increase. So it would not be a big problem. The following year it may swing back to I% = - 6% so then D% switches to +10% making payments fall by 10% relative to incomes. As a trend, the falls in the payments are always bigger then the rises.
Alternatively, lenders can observe that a one year spike of 11% in I% would take D% to -7% (say) making the cost of repayments rise by 7% more than incomes are rising. This is less than the worst case result for a Level Payments Mortgage after a 1% interest rate increase. So it would not be a big problem. The following year it may swing back to I% = - 6% so then D% switches to +10% making payments fall by 10% relative to incomes. As a trend, the falls in the payments are always bigger then the rises.
ESTIMATING THE MAXIMUM I%
The best way to set the Safe Entry cost appears to be to set it by estimating the maximum sustainable value of I% for the economy and the lending industry concerned. It is likely that this maximum value is likely to be less than the true rate of return (above AEG%) on other investments which are more risky.
For UK and USA Equities this may be less than say 5% p.a. true (above AEG% p.a.) and less than that for property, but the detailed studies of past data seem to show that the sustainable value of I% has to be positive above AEG% p.a. by around 2% or more to prevent inflation from running out of control.
For UK and USA Equities this may be less than say 5% p.a. true (above AEG% p.a.) and less than that for property, but the detailed studies of past data seem to show that the sustainable value of I% has to be positive above AEG% p.a. by around 2% or more to prevent inflation from running out of control.
This does not mean that 'Sustainable I%' or the Median value if 'I%' will stay within those narrow limits, between about 2% and 4% for the UK. It does mean that it will not deviate far for very long. Tests show that short term deviations from mean, even large ones, can be accommodated as just outlined and as readers will see in the illustrations to be given in the later pages (writing in progress).
As already stated, the worst that can happen is that P% and so P, the current monthly payments, may have to make some upwards adjustment, if I% moves above the anticipated range and stays there, just as happens with the current variable rate Level Payments (LP) mortgage model, but more likely current ILS mortgages will be allowed to extend their repayment period and new mortgages will cost more.
As already stated, the worst that can happen is that P% and so P, the current monthly payments, may have to make some upwards adjustment, if I% moves above the anticipated range and stays there, just as happens with the current variable rate Level Payments (LP) mortgage model, but more likely current ILS mortgages will be allowed to extend their repayment period and new mortgages will cost more.
SETTING D%
Setting D% is another issue. Consider how volatile income increases are so that D% is large enough to cope with that. More volatile pay rises means that there will be a larger variation (standard deviation maybe) among individuals' wage increases, requiring D% to be increased so as to cope with the laggards.
The critical value for D%, the value when too many borrowers will be unable to cope, (too many may be 5% or more - it is a matter of culture, politics, and opinion), needs local researches to be done to see how far adrift - how far behind the average - an individual borrower's income may lag behind the index selected. See the page on Defining the index for more on that.
The critical value for D%, the value when too many borrowers will be unable to cope, (too many may be 5% or more - it is a matter of culture, politics, and opinion), needs local researches to be done to see how far adrift - how far behind the average - an individual borrower's income may lag behind the index selected. See the page on Defining the index for more on that.
As mentioned earlier, we want to leave C% alone when I% increases so that the mortgage is repaid on time. So the value of D% will take the strain. If we use too low a value for I% when we set the entry cost value of P% (the first year value), then as I% rises to its maximum sustainable level, D% will fall too low to be comfortable.
Either the value of P% will have to jump up as it does with the current variable interest rate mortgages, or there will be payments fatigue and there will be arrears. And probably the new entry cost for new mortgages will be high and property values will fall endangering collateral security, besides re-distributing wealth among the population.
Either the value of P% will have to jump up as it does with the current variable interest rate mortgages, or there will be payments fatigue and there will be arrears. And probably the new entry cost for new mortgages will be high and property values will fall endangering collateral security, besides re-distributing wealth among the population.
For most economies that are reasonably stable, the initial / entry cost value of P% based on these considerations ought to be reasonably stable because the median value of I% used in the entry cost calculation will also be stable. In the UK my opinion is that it would lie between 2% and 3% and stay there for decades unless something fundamental changes, possibly like the new regulations coming in that would raise lending costs, and a 4% value of D% mimics incomes rising at 4% p.a. (whether they are rising or falling), which looking at past records suggests a very low, almost invisible rate of arrears.
So in such a case,
P% = 1.5% or similar, + 4% (D%) + 3% (I% sustainable) = 8.5% and stable.
The mortgage multiple would be 3.5 years' income and stable, rising in a proportionate way as incomes rise. As mentioned earlier, the Country Report from the IMF in July 2012 stated that long term UK property prices had averaged 3.5 years' income. And in those days 100% mortgages were on offer.
P% = 1.5% or similar, + 4% (D%) + 3% (I% sustainable) = 8.5% and stable.
The mortgage multiple would be 3.5 years' income and stable, rising in a proportionate way as incomes rise. As mentioned earlier, the Country Report from the IMF in July 2012 stated that long term UK property prices had averaged 3.5 years' income. And in those days 100% mortgages were on offer.
MAJOR BREAKTHROUGH
This means that the amount of wealth (income multiple) lent and the cost of housing will rise with rising incomes / aggregate demand, which is what every other good and service and rentals may be expected to do, ceteris paribus.
THAT is a major breakthrough on its own. The whole spending and cost patterns in the economy can harmonize. Wealth gets safer and costs become easier to forecast.
It takes out a lot of arrears risk, collateral security risk, and wealth re-distribution for the community. It puts the construction industry onto a secure footing. It helps the whole economy to grow.
This means that the value of property used as collateral will not bubble and burst, but will remain sufficiently stable that a 100% mortgage may not be out of the question. Even more than 100% can be lent in some conditions based upon the presumption that a borrower does not wish to abandon his/her home and end up owing money as well. This depends on the law of the land supporting the lender, and the cultural attitude to debt.
====================
INDEXATION
The AEG% part of the interest can also be replaced with indexation. Adding AEG% interest to a debt is the same as index-linking to AEG% p.a. In the absence of any payments, both methods increase the value of the debt by AEG% p.a.
In other words AEG% interest or indexation increases the debt at the same pace as average incomes are rising. The debt / income ratio does not change. If a year's income has been lent then many years later if no payments have been made, a years' income is still owed but it will be more in money terms because both debt and incomes are bigger.
For now we are using average incomes, not that of an individual.
SUMMARISING THIS
If I% = 0% what it means is that all the debts are rising as fast as average incomes. Or average incomes are rising as fast as the debt.
This means that the amount of 'average income' that has been borrowed is the same as the amount of 'average income' that gets repaid.
You can say the same thing about national / government debt. Replace AEG% with the rate of growth of GDP, assuming that tax revenues will rise as fast as GDP as an approximation. Then:
If 1 GDP is borrowed and if net tax revenues are rising as fast as GDP is rising, then after a year the amount of the debt is still going to be 1 GDP. If this happens then we could say that the Government's marginal interest rate above GDP rate of growth p.a., I% = 0%. A different but almost identical definition of I% based on GDP instead of AEG.
There is no marginal, or additional interest to be paid. The nominal interest added is the same as the rate of growth of net income or GDP.
To see the role that is played by I% let's look at a spreadsheet example. Here I% = 0%:
The loan starts at 100 000 in any currency, adds 5% interest, subtracts a payment and ends with a balance at the end of the year. This balance is taken down to the start of year 2 and the process is repeated.
To make sense of this, the interest is added at year end and that is when the payment is made by which time incomes have risen by AEG% = 5% in this case. As a percentage of that new income the cost of the payment is shown in the final column.
By adding up those final column percentages we find out the cost-to-income of repaying the loan, which comes to one year's income as shown in the bottom line.
We can either add up the money repaid, which is 110,163 as shown and is 10.2% more than was borrowed, or we can add up the '% of income' column which calculates how much income is needed to make the payments. This shows that 1 year's income was borrowed and 1 year's income was needed to repay. Zero cost to income - at least in theory assuming that the income rises at AEG% p.a. all the time.
If you add up the money, it looks expensive: 10.2% more than was borrowed.
NOTE: The payment is made after the interest is added, both being at year's end by which time the income has risen by AEG%. Hence the fourth year's income is shown.
The net cost-to-income is 0% as shown.
EXAMPLE 2 - If I% is positive at 3% we get this after one year:
The amount of income added to the debt in the first year is I% x L, or 3% times three years' income = 9% of a year's income. The debt is repaid at the end of the first year in this example.
Now we see that maybe it is of use to count cost in terms of income rather than in terms of money. Food for thought. Something to explore. Let's do that. Let's think about this:
WEALTH / INCOME?
If we look at this from the viewpoint of the lender or the investor in the debt, (think of savers as investors using deposits or think of investors in bonds that are used to provide mortgages), we see from the above example where I% was 3%, that I% is the rate of increase in the debt in units of average income, or wealth (income) that was lent. I am associating income and wealth with each other as being in some way the same thing.
If r% = AEG% p.a. then the lent income , say a year's income, returns as a year's current, spendable income that has been preserved by the addition of interest at the rate at which incomes have been growing.
I will explain that more as we get to more illustrations because usually people do not think of wealth in this way. This is where people get a bit dizzy sometimes. But stay calm, relax, and watch what else the figures will tell us as we progress.
There is of course the fact that if prices are rising more slowly than incomes (which may not always be the case), the purchasing power of a year's income will be rising. I make a distinction between purchasing power, which rises or falls for everyone at the same pace, and wealth / stored / lent income which either gets repaid, repaid with interest, or repaid in part because interest was less than AEG% p.a.
If a borrower repays less income than was lent then he/she can spend the income that was borrowed and repay less income / wealth, leaving him/her with a surplus. The lender loses the same amount. Thus the wealth is shifted, not destroyed. It remains a constant - the share of national income which each person has as total national incomes increase or decrease is the total wealth creation of the nation at any one time. Each person has a share, and every investment can be measured as a share of that total national wealth / income. Its value may be rising or falling as prices rise or fall faster or slower than incomes, but as a share of the national wealth it is incomes that define it. And when it comes to mortgages, these are repaid out of incomes, so if income is added to the debt by a positive value of I% this matters. It can make a mortgage unaffordable if I% is too large or if the mortgage debt is too large.
INVESTOR'S CHOICE
Let us say that the lender views average incomes as the measure of wealth that is invested. If the lender were a person and wanted to invest in something else, then among other things, there would be a choice of property and equities both of which have a link to aggregate demand / average incomes. Most goods and services respond in price to the level of demand and aggregate demand is at least, loosely linked to average incomes / earnings and thus to Average Earnings Growth, AEG.
So we have now found that AEG% p.a. forms a baseline - a way to compare all investments and how fast they grow. Anything that grows as fast as AEG% p.a. preserves the income that was invested in it.
We can compare AEG% p.a. to the rate of capital growth of an investment and we can compare I% to the dividends or the rental income obtained from such investments. The assumption is that rising incomes, rising AEG% p.a., will result in rising rentals and profits and rising turnover and that this will raise the base value of property and Equities at the base rate of AEG% p.a.
WEALTH BONDS
Clearly, if there was a risk free bond that rose at AEG% p.a. this would be a baseline against which all investments could be compared. I have named such bonds, risk free or not, 'Wealth Bonds' because they preserve the income that is saved in them, and because if that income is not preserved then another person will spend it - or will spend the part that was lost as I already explained and as we will see in another illustration below.
Now think about that. If that were not true, if the total wealth owed and repaid was not preserved, then we might not be so sure of calling this lent income a form of wealth. But if that wealth, that stored income that is lent, is going to be given in part to the borrower to spend, and not just eroded by inflation of incomes, then we must conclude that it has been preserved and that this is indeed something that has a character of its own. I will call that characteristic the property of conservation of wealth.
CONSERVATION OF WEALTH
So we have a conservation law - conservation of wealth. Wealth (spendable income), as defined here, does not vanish - it gets transferred. Where did you read that in your text books? Another Eureka!
That is not true of an investment in goods like gold or in property or in equities. The wealth invested in them depends upon there being a willing buyer at the price on offer. The wealth invested in a bond is a call upon the income of the borrower which is clearly defined.
In fact, all wealth, even that invested in property gold, equities, bonds etc is a call upon the income of a willing buyer. The money given for purchase is spendable as income and it comes either from the stored income or the current income of the buyer, or some of each.
With a mortgage the I% additional interest above the AEG% index is the dividend, or the rental, as far as the investor is concerned, but as just mentioned there is no real volatility in the actual wealth lent / invested when it comes to loans / bonds. It is not volatile at all in the sense that their value is not dependent upon there being a willing buyer. The loan contract constitutes a call on the future income of the borrower, willing or not. Able or not is another question and therein lies the risk. But as long as the borrower is able to pay or has collateral with which to pay, a bond just preserves the wealth that has been lent and adds to it in a secure and profitable way as long as I% is positive.
But if I% is negative and r% is less than AEG% p.a. then wealth moves from lender to borrower.
COMPETING FOR FUNDS
Lenders have to compete for funds with these other investments such as property and equities. They have an advantage - their loans are secured. The risk of lending is very low and if we have a positive D% p.a. built in then the level of arrears will be low too. This can be the basis for an AAA rated investment in mortgage based securities.
A ten year bond with a fixed I% would attract a lot of money from investors wanting to get out of the uncertainties of inflation.
A bond that has a fixed I% p.a. takes the investor out of the turmoil in the economy and protects the wealth that has been invested.
Such bonds are called Wealth Bonds.
SUMMARY OF PART 2
We have noted that AEG% p.a. forms a baseline for aggregate demand in an economy. GDP growth is also a form of AEG% p.a. because GDP is defined as aggregate income, like aggregate AEG when it comes to the rate of growth. This does not always work out exactly - the figures are not always exactly the same because of differences in definitions and in the timing of measurements and revisions to measurements, but there are strong similarities.
I did a test for South Africa's non farm wages index and found that GDP and that wages index both rose by almost the same amount over a 25 year period, with a 5% cumulative difference. Some years the differences were greater than others. But it needs to be noted that GDP varies as the number of working people in the population changes, so immigration and emigration makes a difference, as does demographics - an aging population or a young population, can for example, affect GDP.
If interest equal to AEG% p.a. is added then the amount of 'average income' owed never changes. Only the addition of a marginal rate of interest called the true rate of interest, I%, increases the amount of income (wealth) owed.
A ten year fixed true rate bond would attract a lot of funds from older people and their pension funds and some of their managed funds. The same with 15 year bonds, and even 25 year bonds. Some people would buy wealth bonds directly for themselves. Some wealth bonds would repay capital as well as paying interest so as to provide an annuity or to provide fund managers with a higher cash flow which they like to have. It helps them to re-balance their fund as needed. We will see how that kind of bond is the other side of a fixed true interest rate mortgage, called a Defined Cost Mortgage.
MANAGING INFLATION
Central banks have the task of managing inflation and they use interest rates to manage the level of demand for money. Because banks can leverage their lending - that is to say they can create new money by lending more than the assets that they hold, the rate of interest limits the amount of money that can be lent. That limits the growth of money supply.
This means that it is very important that I% should be positive if there is to be a significant cost of borrowing. Otherwise the demand for loans will exceed the supply, or the demand for loans will be so great as to force the Central Bank to increase interest rates to prevent an inflationary spiral caused by run-away borrowing and credit creation.
Imagine being able to borrow at AEG% interest and then invest in property at AEG% p.a. growth and get rental on top - for example. Everyone would start doing that eventually. The whole economy would run wild and everything would collapse in hyper-inflation.
At the same time, I% must not be too high for too long because it will make lending produce a secure return that is greater than that which can be obtained by investing in property or equities and without the risk. The result will be a flood of money that is too expensive to lend. Borrowers will be unable to afford such an expense.
So one way or another market forces keep true interest rates in a very narrow band, except when they wander off course for a while in both directions. The reasons for that wandering is the subject of conjecture at this time, but instinctively one knows that is is caused by the instabilities in economies, instabilities largely caused by the debt structures. And then the over-response and unbalanced responses made by Central Banks and their unbalanced instruments of intervention.
These are things I write about when discussing monetary policy in the new and the old environment, before and after these new debt structures are introduced.
Studies done on the UK, and other places (but mainly the UK) suggest that over a business cycle, on average, I% has to lie between 2% and 4% unless the Central Bank has distorted interest rates or other factors have done so. For example Quantitative Easing or an excess of foreign money coming in can lower interest rates for several years. Such distortions can greatly extend the business cycle which is why I chose to say the average rate of I% will tend to lie in this narrow range 'over a business cycle'.
Another distorting factor when raising the interest rate would precipitate a housing crisis or an economic slowdown. That is what happens with the current mortgage models. The first scenario (the crisis) is what the Fed discovered, and the second scenario (a failure to raise the interest rate enough to slow inflation) is what the Bank of England discovered, making them reduce interest rates and miss the inflation target in circa 2004 - I have the charts.
The problem arises because if the Fed had had its way the monthly payments cost P p.a. of USA mortgages would have risen by 58%! Not much like a rental mortgage model, is it?
Such changes, and lesser changes that exceed the baseline of other price changes such as rentals and goods and services change spending patterns as well as wealth patterns (as property values bubble and crash). And when spending shifts from one sector to another it destroys jobs. When the wealth invested in property and other investments follows the same direction as interest rates rise and fall, and with all of that alternating in direction, that re-enforces the trend and enlarges the business cycle significantly. This is a barrier to the achievement of sustained economic growth.
As we will see later, with the ILS Model and risk management methods, these problems of rapidly changing mortgage costs and mortgage sizes (loan/income ratios) would be removed. Goodbye to at least some of the interest rate based distortions in our economies.
The upper true interest rate bound of 4% is for the UK and the USA where banking has been efficient. It may be more costly in future so watch out - BASEL III etc to blame here. This is because the long term rate of return on Equities has been around 7% p.a. in real terms. See the study on Siegel's Constant and other studies that came up with similar figures over 200 years.
This true rate of return on equities may be less than 5% p.a. - that is above AEG% p.a. The difference between real and true rates of return is because incomes rise faster than prices most of the time. I will come back to that a bit later to make sure this difference is clear and well understood. I also go into that in detail on the Siegel's Constant page just mentioned.
It means that if an investment keeps pace with AEG it also keeps pace with real economic growth and it needs to do that to preserve the wealth that has been invested - to stop some of it escaping to be spent by others.
REMOVING DISTORTIONS
Distorting interest rates leads to unsustainable imbalances in the economy. It redistributes wealth and does harm. Readers should bear this in mind as they read further because my new debt structures should remove the need for distorted interest rates, which are usually used to reduce the rate of default on debts (as just mentioned) which mainly occur in the housing sector insofar as this sector is the most disturbed by interest rate increases and decreases. This also forms a barrier to the Central Bank's interest rate policy.
If we can manage to find a way of keeping D% positive even as interest rates are rising, then interest rates can be free to rise without causing arrears. The exciting part is that tests show that we can do that.
The secret is that for every 1% increase in the true interest rate D% has to fall by 1% if P% and C% are not to be disturbed:
P% = C% + D% + I%
So if the true rate can only rise by 2% at most from it long term average rate, then D% can always be at least 2% positive if it starts out as 4% for a new mortgage. Short term extremes in I% can be smoothed out by the averaging process as we will see in the illustrations to come.
THE BENEFITS OF REMOVING DISTORTIONS
In short, the other exciting thing that I discovered after much analysis and careful thinking was that, with these new debt structures in place, major economic interventions and such distortions need not happen and should not be tolerated. When we take out the distortions that are caused both directly and indirectly in this way by the debt structures which are currently in use, the economy should behave well and such interventions (for example also a Keynesian stimulus) should not need to be large, even if one is actually needed.
An economy that has secure borrowing and secure wealth with stability in its finances, should be an economy in which almost everyone wants to spend more to get more and so everyone starts to earn more as they provide more for one another. That is how it works eventually, but with financial stability, that is how it should work all the time - other than after currency crises and natural disasters.
SUMMARYI say that a stimulus may not be needed in this case after careful consideration of how business cycles get amplified by a combination of the instability of mortgage finance and bond values as interest rates change. This is then further amplified by the 'wealth effect' and a general lack of confidence which results. Everything reverses including the wealth (greed and panic) effect when property prices and bond values shoot upwards again. This sets the scene for the next crisis as interest rates start rising once more.
If we can get rid of these amplifications and distortions, then I% should also be stable. But in the meantime we have to deal with unstable I% and we have to be sure that the new mortgage model can cope with that. The outcome of my detailed studies shows that this is all quite possible.
SUMMARY OF PART 3
We saw that if the true rate of interest is very low it will cause over-lending and inflation. And if the true interest rate is kept above around 4% for very long, it will result in such a high demand for deposits and bonds by investors that lenders will be unable to lend the money on deposit and in bonds. Free markets do not permit this kind of thing.
We noted that if the true interest rate is higher than the long term rate of return on equities then a 10 year true rate bond issue would be over-subscribed many times. Lenders could not lend that much at that cost to borrowers.
Thus true interest rates are largely confined to a narrow range over the medium to long term, which my historic data seems to confirm. I WILL PROVIDE THE CHARTS FOR SOME OF THESE STATISTICS ON ANOTHER PAGE SHORTLY. And historic data for a number of nations can be found on my interactive spreadsheets that are for sale.
BY THE WAY...
Spreadsheet owners can run any number of tests on the data and many fascinating tests are suggested. One test shows that if interest rates and AEG rates rise every year by 1% p.a. starting at 3% interest and 0% AEG, the ILS Mortgage model does not really notice that happening. It is not at all disturbed!
Whatever the rate of AEG% p.a. is doing, if I% p.a. is fixed then D% p.a. is fixed and you get what I call a Defined Cost Mortgage (fixed I% and fixed D%) like this:

The shapes and slopes do not alter with varying AEG% p.a. not with external rates of interest. Users can put any figures into my interactive spreadsheets and see what happens to both the ILS and the traditional mortgage models. Results are displayed on ten different Bar Charts as well as full tabulations.
SUMMARY CONTINUED
Interest rate distortions were mentioned, which relate to the instability of mortgage payments as currently constructed. For example the current practice of linking the amount lent to the nominal rate of interest results in a great deal of instability in the loan/income ratio (mortgage sizes), and so affecting property values and interest rate changes hugely increases the risk of borrowing arrears when variable rates are used. These distortions to interest rates and property values feed into the economy and get amplified by the wealth effect making everything unstable.
Let's get back to the maths now:
INDEXATION
The AEG% part of the interest can also be replaced with indexation. Adding AEG% interest to a debt is the same as index-linking to AEG% p.a. In the absence of any payments, both methods increase the value of the debt by AEG% p.a.
In other words AEG% interest or indexation increases the debt at the same pace as average incomes are rising. The debt / income ratio does not change. If a year's income has been lent then many years later if no payments have been made, a years' income is still owed but it will be more in money terms because both debt and incomes are bigger.
For now we are using average incomes, not that of an individual.
SUMMARISING THIS
If I% = 0% what it means is that all the debts are rising as fast as average incomes. Or average incomes are rising as fast as the debt.
This means that the amount of 'average income' that has been borrowed is the same as the amount of 'average income' that gets repaid.
You can say the same thing about national / government debt. Replace AEG% with the rate of growth of GDP, assuming that tax revenues will rise as fast as GDP as an approximation. Then:
If 1 GDP is borrowed and if net tax revenues are rising as fast as GDP is rising, then after a year the amount of the debt is still going to be 1 GDP. If this happens then we could say that the Government's marginal interest rate above GDP rate of growth p.a., I% = 0%. A different but almost identical definition of I% based on GDP instead of AEG.
There is no marginal, or additional interest to be paid. The nominal interest added is the same as the rate of growth of net income or GDP.
To see the role that is played by I% let's look at a spreadsheet example. Here I% = 0%:
The loan starts at 100 000 in any currency, adds 5% interest, subtracts a payment and ends with a balance at the end of the year. This balance is taken down to the start of year 2 and the process is repeated.
To make sense of this, the interest is added at year end and that is when the payment is made by which time incomes have risen by AEG% = 5% in this case. As a percentage of that new income the cost of the payment is shown in the final column.
By adding up those final column percentages we find out the cost-to-income of repaying the loan, which comes to one year's income as shown in the bottom line.
We can either add up the money repaid, which is 110,163 as shown and is 10.2% more than was borrowed, or we can add up the '% of income' column which calculates how much income is needed to make the payments. This shows that 1 year's income was borrowed and 1 year's income was needed to repay. Zero cost to income - at least in theory assuming that the income rises at AEG% p.a. all the time.
If you add up the money, it looks expensive: 10.2% more than was borrowed.
NOTE: The payment is made after the interest is added, both being at year's end by which time the income has risen by AEG%. Hence the fourth year's income is shown.
The net cost-to-income is 0% as shown.
EXAMPLE 2 - If I% is positive at 3% we get this after one year:
The amount of income added to the debt in the first year is I% x L, or 3% times three years' income = 9% of a year's income. The debt is repaid at the end of the first year in this example.
Now we see that maybe it is of use to count cost in terms of income rather than in terms of money. Food for thought. Something to explore. Let's do that. Let's think about this:
WEALTH / INCOME?
If we look at this from the viewpoint of the lender or the investor in the debt, (think of savers as investors using deposits or think of investors in bonds that are used to provide mortgages), we see from the above example where I% was 3%, that I% is the rate of increase in the debt in units of average income, or wealth (income) that was lent. I am associating income and wealth with each other as being in some way the same thing.
If r% = AEG% p.a. then the lent income , say a year's income, returns as a year's current, spendable income that has been preserved by the addition of interest at the rate at which incomes have been growing.
I will explain that more as we get to more illustrations because usually people do not think of wealth in this way. This is where people get a bit dizzy sometimes. But stay calm, relax, and watch what else the figures will tell us as we progress.
There is of course the fact that if prices are rising more slowly than incomes (which may not always be the case), the purchasing power of a year's income will be rising. I make a distinction between purchasing power, which rises or falls for everyone at the same pace, and wealth / stored / lent income which either gets repaid, repaid with interest, or repaid in part because interest was less than AEG% p.a.
If a borrower repays less income than was lent then he/she can spend the income that was borrowed and repay less income / wealth, leaving him/her with a surplus. The lender loses the same amount. Thus the wealth is shifted, not destroyed. It remains a constant - the share of national income which each person has as total national incomes increase or decrease is the total wealth creation of the nation at any one time. Each person has a share, and every investment can be measured as a share of that total national wealth / income. Its value may be rising or falling as prices rise or fall faster or slower than incomes, but as a share of the national wealth it is incomes that define it. And when it comes to mortgages, these are repaid out of incomes, so if income is added to the debt by a positive value of I% this matters. It can make a mortgage unaffordable if I% is too large or if the mortgage debt is too large.
INVESTOR'S CHOICE
Let us say that the lender views average incomes as the measure of wealth that is invested. If the lender were a person and wanted to invest in something else, then among other things, there would be a choice of property and equities both of which have a link to aggregate demand / average incomes. Most goods and services respond in price to the level of demand and aggregate demand is at least, loosely linked to average incomes / earnings and thus to Average Earnings Growth, AEG.
So we have now found that AEG% p.a. forms a baseline - a way to compare all investments and how fast they grow. Anything that grows as fast as AEG% p.a. preserves the income that was invested in it.
We can compare AEG% p.a. to the rate of capital growth of an investment and we can compare I% to the dividends or the rental income obtained from such investments. The assumption is that rising incomes, rising AEG% p.a., will result in rising rentals and profits and rising turnover and that this will raise the base value of property and Equities at the base rate of AEG% p.a.
WEALTH BONDS
Clearly, if there was a risk free bond that rose at AEG% p.a. this would be a baseline against which all investments could be compared. I have named such bonds, risk free or not, 'Wealth Bonds' because they preserve the income that is saved in them, and because if that income is not preserved then another person will spend it - or will spend the part that was lost as I already explained and as we will see in another illustration below.
Now think about that. If that were not true, if the total wealth owed and repaid was not preserved, then we might not be so sure of calling this lent income a form of wealth. But if that wealth, that stored income that is lent, is going to be given in part to the borrower to spend, and not just eroded by inflation of incomes, then we must conclude that it has been preserved and that this is indeed something that has a character of its own. I will call that characteristic the property of conservation of wealth.
CONSERVATION OF WEALTH
So we have a conservation law - conservation of wealth. Wealth (spendable income), as defined here, does not vanish - it gets transferred. Where did you read that in your text books? Another Eureka!
That is not true of an investment in goods like gold or in property or in equities. The wealth invested in them depends upon there being a willing buyer at the price on offer. The wealth invested in a bond is a call upon the income of the borrower which is clearly defined.
In fact, all wealth, even that invested in property gold, equities, bonds etc is a call upon the income of a willing buyer. The money given for purchase is spendable as income and it comes either from the stored income or the current income of the buyer, or some of each.
With a mortgage the I% additional interest above the AEG% index is the dividend, or the rental, as far as the investor is concerned, but as just mentioned there is no real volatility in the actual wealth lent / invested when it comes to loans / bonds. It is not volatile at all in the sense that their value is not dependent upon there being a willing buyer. The loan contract constitutes a call on the future income of the borrower, willing or not. Able or not is another question and therein lies the risk. But as long as the borrower is able to pay or has collateral with which to pay, a bond just preserves the wealth that has been lent and adds to it in a secure and profitable way as long as I% is positive.
But if I% is negative and r% is less than AEG% p.a. then wealth moves from lender to borrower.
COMPETING FOR FUNDS
Lenders have to compete for funds with these other investments such as property and equities. They have an advantage - their loans are secured. The risk of lending is very low and if we have a positive D% p.a. built in then the level of arrears will be low too. This can be the basis for an AAA rated investment in mortgage based securities.
A ten year bond with a fixed I% would attract a lot of money from investors wanting to get out of the uncertainties of inflation.
A bond that has a fixed I% p.a. takes the investor out of the turmoil in the economy and protects the wealth that has been invested.
Such bonds are called Wealth Bonds.
SUMMARY OF PART 2
We have noted that AEG% p.a. forms a baseline for aggregate demand in an economy. GDP growth is also a form of AEG% p.a. because GDP is defined as aggregate income, like aggregate AEG when it comes to the rate of growth. This does not always work out exactly - the figures are not always exactly the same because of differences in definitions and in the timing of measurements and revisions to measurements, but there are strong similarities.
I did a test for South Africa's non farm wages index and found that GDP and that wages index both rose by almost the same amount over a 25 year period, with a 5% cumulative difference. Some years the differences were greater than others. But it needs to be noted that GDP varies as the number of working people in the population changes, so immigration and emigration makes a difference, as does demographics - an aging population or a young population, can for example, affect GDP.
If interest equal to AEG% p.a. is added then the amount of 'average income' owed never changes. Only the addition of a marginal rate of interest called the true rate of interest, I%, increases the amount of income (wealth) owed.
A ten year fixed true rate bond would attract a lot of funds from older people and their pension funds and some of their managed funds. The same with 15 year bonds, and even 25 year bonds. Some people would buy wealth bonds directly for themselves. Some wealth bonds would repay capital as well as paying interest so as to provide an annuity or to provide fund managers with a higher cash flow which they like to have. It helps them to re-balance their fund as needed. We will see how that kind of bond is the other side of a fixed true interest rate mortgage, called a Defined Cost Mortgage.
PART 3
True rates are confined to a narrow band
The economics of Interest rates
The economics of Interest rates
MANAGING INFLATION
Central banks have the task of managing inflation and they use interest rates to manage the level of demand for money. Because banks can leverage their lending - that is to say they can create new money by lending more than the assets that they hold, the rate of interest limits the amount of money that can be lent. That limits the growth of money supply.
This means that it is very important that I% should be positive if there is to be a significant cost of borrowing. Otherwise the demand for loans will exceed the supply, or the demand for loans will be so great as to force the Central Bank to increase interest rates to prevent an inflationary spiral caused by run-away borrowing and credit creation.
Imagine being able to borrow at AEG% interest and then invest in property at AEG% p.a. growth and get rental on top - for example. Everyone would start doing that eventually. The whole economy would run wild and everything would collapse in hyper-inflation.
At the same time, I% must not be too high for too long because it will make lending produce a secure return that is greater than that which can be obtained by investing in property or equities and without the risk. The result will be a flood of money that is too expensive to lend. Borrowers will be unable to afford such an expense.
So one way or another market forces keep true interest rates in a very narrow band, except when they wander off course for a while in both directions. The reasons for that wandering is the subject of conjecture at this time, but instinctively one knows that is is caused by the instabilities in economies, instabilities largely caused by the debt structures. And then the over-response and unbalanced responses made by Central Banks and their unbalanced instruments of intervention.
These are things I write about when discussing monetary policy in the new and the old environment, before and after these new debt structures are introduced.
Studies done on the UK, and other places (but mainly the UK) suggest that over a business cycle, on average, I% has to lie between 2% and 4% unless the Central Bank has distorted interest rates or other factors have done so. For example Quantitative Easing or an excess of foreign money coming in can lower interest rates for several years. Such distortions can greatly extend the business cycle which is why I chose to say the average rate of I% will tend to lie in this narrow range 'over a business cycle'.
Another distorting factor when raising the interest rate would precipitate a housing crisis or an economic slowdown. That is what happens with the current mortgage models. The first scenario (the crisis) is what the Fed discovered, and the second scenario (a failure to raise the interest rate enough to slow inflation) is what the Bank of England discovered, making them reduce interest rates and miss the inflation target in circa 2004 - I have the charts.
The problem arises because if the Fed had had its way the monthly payments cost P p.a. of USA mortgages would have risen by 58%! Not much like a rental mortgage model, is it?
Such changes, and lesser changes that exceed the baseline of other price changes such as rentals and goods and services change spending patterns as well as wealth patterns (as property values bubble and crash). And when spending shifts from one sector to another it destroys jobs. When the wealth invested in property and other investments follows the same direction as interest rates rise and fall, and with all of that alternating in direction, that re-enforces the trend and enlarges the business cycle significantly. This is a barrier to the achievement of sustained economic growth.
As we will see later, with the ILS Model and risk management methods, these problems of rapidly changing mortgage costs and mortgage sizes (loan/income ratios) would be removed. Goodbye to at least some of the interest rate based distortions in our economies.
The upper true interest rate bound of 4% is for the UK and the USA where banking has been efficient. It may be more costly in future so watch out - BASEL III etc to blame here. This is because the long term rate of return on Equities has been around 7% p.a. in real terms. See the study on Siegel's Constant and other studies that came up with similar figures over 200 years.
This true rate of return on equities may be less than 5% p.a. - that is above AEG% p.a. The difference between real and true rates of return is because incomes rise faster than prices most of the time. I will come back to that a bit later to make sure this difference is clear and well understood. I also go into that in detail on the Siegel's Constant page just mentioned.
It means that if an investment keeps pace with AEG it also keeps pace with real economic growth and it needs to do that to preserve the wealth that has been invested - to stop some of it escaping to be spent by others.
REMOVING DISTORTIONS
Distorting interest rates leads to unsustainable imbalances in the economy. It redistributes wealth and does harm. Readers should bear this in mind as they read further because my new debt structures should remove the need for distorted interest rates, which are usually used to reduce the rate of default on debts (as just mentioned) which mainly occur in the housing sector insofar as this sector is the most disturbed by interest rate increases and decreases. This also forms a barrier to the Central Bank's interest rate policy.
If we can manage to find a way of keeping D% positive even as interest rates are rising, then interest rates can be free to rise without causing arrears. The exciting part is that tests show that we can do that.
The secret is that for every 1% increase in the true interest rate D% has to fall by 1% if P% and C% are not to be disturbed:
P% = C% + D% + I%
So if the true rate can only rise by 2% at most from it long term average rate, then D% can always be at least 2% positive if it starts out as 4% for a new mortgage. Short term extremes in I% can be smoothed out by the averaging process as we will see in the illustrations to come.
THE BENEFITS OF REMOVING DISTORTIONS
In short, the other exciting thing that I discovered after much analysis and careful thinking was that, with these new debt structures in place, major economic interventions and such distortions need not happen and should not be tolerated. When we take out the distortions that are caused both directly and indirectly in this way by the debt structures which are currently in use, the economy should behave well and such interventions (for example also a Keynesian stimulus) should not need to be large, even if one is actually needed.
An economy that has secure borrowing and secure wealth with stability in its finances, should be an economy in which almost everyone wants to spend more to get more and so everyone starts to earn more as they provide more for one another. That is how it works eventually, but with financial stability, that is how it should work all the time - other than after currency crises and natural disasters.
SUMMARYI say that a stimulus may not be needed in this case after careful consideration of how business cycles get amplified by a combination of the instability of mortgage finance and bond values as interest rates change. This is then further amplified by the 'wealth effect' and a general lack of confidence which results. Everything reverses including the wealth (greed and panic) effect when property prices and bond values shoot upwards again. This sets the scene for the next crisis as interest rates start rising once more.
If we can get rid of these amplifications and distortions, then I% should also be stable. But in the meantime we have to deal with unstable I% and we have to be sure that the new mortgage model can cope with that. The outcome of my detailed studies shows that this is all quite possible.
SUMMARY OF PART 3
We saw that if the true rate of interest is very low it will cause over-lending and inflation. And if the true interest rate is kept above around 4% for very long, it will result in such a high demand for deposits and bonds by investors that lenders will be unable to lend the money on deposit and in bonds. Free markets do not permit this kind of thing.
We noted that if the true interest rate is higher than the long term rate of return on equities then a 10 year true rate bond issue would be over-subscribed many times. Lenders could not lend that much at that cost to borrowers.
Thus true interest rates are largely confined to a narrow range over the medium to long term, which my historic data seems to confirm. I WILL PROVIDE THE CHARTS FOR SOME OF THESE STATISTICS ON ANOTHER PAGE SHORTLY. And historic data for a number of nations can be found on my interactive spreadsheets that are for sale.
BY THE WAY...
Spreadsheet owners can run any number of tests on the data and many fascinating tests are suggested. One test shows that if interest rates and AEG rates rise every year by 1% p.a. starting at 3% interest and 0% AEG, the ILS Mortgage model does not really notice that happening. It is not at all disturbed!
Whatever the rate of AEG% p.a. is doing, if I% p.a. is fixed then D% p.a. is fixed and you get what I call a Defined Cost Mortgage (fixed I% and fixed D%) like this:

The shapes and slopes do not alter with varying AEG% p.a. not with external rates of interest. Users can put any figures into my interactive spreadsheets and see what happens to both the ILS and the traditional mortgage models. Results are displayed on ten different Bar Charts as well as full tabulations.
SUMMARY CONTINUED
Interest rate distortions were mentioned, which relate to the instability of mortgage payments as currently constructed. For example the current practice of linking the amount lent to the nominal rate of interest results in a great deal of instability in the loan/income ratio (mortgage sizes), and so affecting property values and interest rate changes hugely increases the risk of borrowing arrears when variable rates are used. These distortions to interest rates and property values feed into the economy and get amplified by the wealth effect making everything unstable.
Let's get back to the maths now:
PART 4
At last - the derivation of the equation
And what this tells us

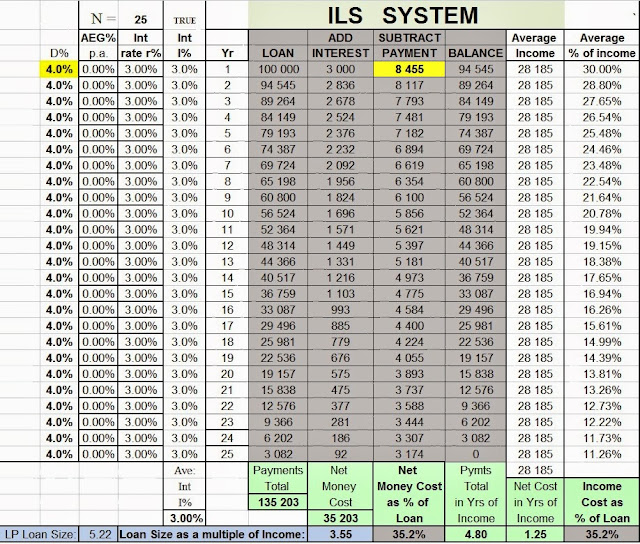







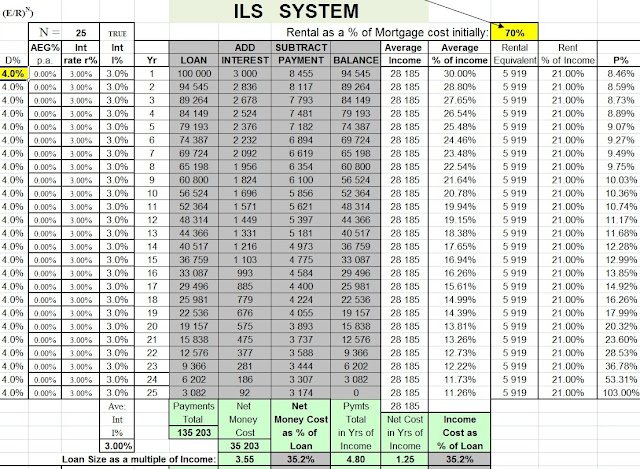



No comments:
Post a Comment
Please type your comment here
Note: Only a member of this blog may post a comment.